题目内容
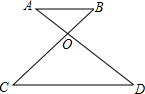 如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )
如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )| A、BO:BC=1:2 |
| B、CD:AB=2:1 |
| C、CO:BC=1:2 |
| D、AD:DO=3:1 |
考点:平行线分线段成比例
专题:
分析:证明△AOB∽△DOC,得到AB:CD=AO:DO=1:2,即可解决问题.
解答: 解:∵AB∥CD,
解:∵AB∥CD,
∴△AOB∽△DOC,
∴AB:CD=AO:DO=1:2,
∴CD:AB=2:1,
故选B.
 解:∵AB∥CD,
解:∵AB∥CD,∴△AOB∽△DOC,
∴AB:CD=AO:DO=1:2,
∴CD:AB=2:1,
故选B.
点评:该题主要考查了平行线分线段成比例定理及其应用问题;解题的关键是判断出△AOB∽△DOC.

练习册系列答案
相关题目
 如图,已知OD平分∠AOB,OE平分∠BOD,若
如图,已知OD平分∠AOB,OE平分∠BOD,若| ∠AOC |
| ∠BOC |
| 3 |
| 2 |
| ∠COE |
| ∠BOE |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列结论错误的是( )
| A、0既不是正数,也不是负数 |
| B、两点之间线段最短 |
| C、锐角和钝角互补 |
| D、两点确定一条直线 |
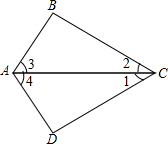 如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )
如图,AC是△ABC和△ADC的公共边,要判定△ABC≌△ADC还需要补充的条件不能是( )| A、AB=AD,∠1=∠2 |
| B、AB=AD,∠3=∠4 |
| C、∠1=∠2,∠3=∠4 |
| D、∠1=∠2,∠B=∠D |
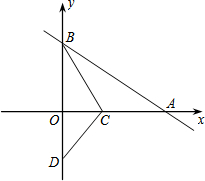 如图:在平面直角坐标系中,直线y=kx+6分别与x轴、y轴交于A、B两点,且OA=8,点C是x轴上一点,如果把△AOB沿着直线BC折叠,那么点A恰好落在y轴负半轴上的点D处.
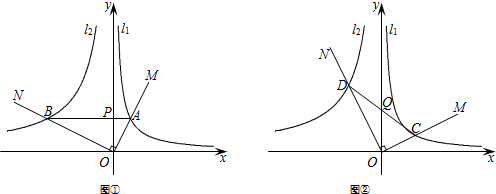
如图:在平面直角坐标系中,直线y=kx+6分别与x轴、y轴交于A、B两点,且OA=8,点C是x轴上一点,如果把△AOB沿着直线BC折叠,那么点A恰好落在y轴负半轴上的点D处.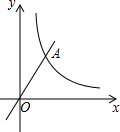 已知图中的曲线是反比例函数y=
已知图中的曲线是反比例函数y=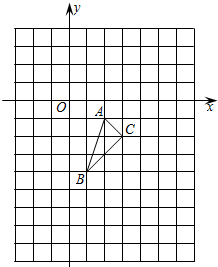 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1)、B(1,-4)、C(3,-2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1)、B(1,-4)、C(3,-2).