题目内容
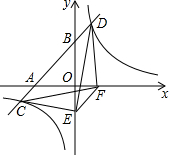 如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=
如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=| 4 |
| x |
①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④AC=BD,其中正确结论的序号是
考点:反比例函数综合题
专题:
分析:①根据函数解析式,可得图象上的点的坐标,根据三角形的面积公式,可得答案;
②根据等第三角形的高相等,可得EF∥CD,根据相似三角形的判定,可得答案;
③根据联立函数解析式,可得方程,根据解方程,可得C、D点的坐标,可得CE与DF的关系,根据自变量与函数值的关系,可得A、B点的坐标,可得∠ABO=∠BAO=45°,根据平行线的性质,可得∠DCE=∠FDA=45°,根据SAS,可得答案;
④根据平行四边的判定与性质,可得BD=EF,AC=BD,可得答案.
②根据等第三角形的高相等,可得EF∥CD,根据相似三角形的判定,可得答案;
③根据联立函数解析式,可得方程,根据解方程,可得C、D点的坐标,可得CE与DF的关系,根据自变量与函数值的关系,可得A、B点的坐标,可得∠ABO=∠BAO=45°,根据平行线的性质,可得∠DCE=∠FDA=45°,根据SAS,可得答案;
④根据平行四边的判定与性质,可得BD=EF,AC=BD,可得答案.
解答:解:①设D(x,
),则F(x,0),
由图象可知x>0,
∴△DEF的面积是:
×|
|×|x|=2,
设C(a,
),则E(0,
),
由图象可知:
<0,a>0,
△CEF的面积是:
×|a|×|
|=2,
∴△CEF的面积=△DEF的面积,
故①正确;
②△CEF和△DEF以EF为底,则两三角形EF边上的高相等,
故EF∥CD,
∴FE∥AB,
∴△AOB∽△FOE,
故②正确;
③∵C、D是一次函数y=x+3的图象与反比例函数y=
的图象的交点,
∴x+3=
,
解得:x=-4或x=1,
经检验:x=-4或1都是原分式方程的解,
∴D(1,4),C(-4,-1),
∴DF=4,CE=4,
∵一次函数y=x+3的图象与x轴,y轴交于A,B两点,
∴A(-3,0),B(0,3),
∴∠ABO=∠BAO=45°,
∵DF∥BO,AO∥CE,
∴∠BCE=∠BAO=45°,∠FDA=∠OBA=45°,
∴∠DCE=∠FDA=45°,
在△DCE和△CDF中
,
∴△DCE≌△CDF(SAS),
故③正确;
④∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,
故④正确;
正确的有4个.
故选:C.
| 4 |
| x |
由图象可知x>0,
∴△DEF的面积是:
| 1 |
| 2 |
| 4 |
| x |
设C(a,
| 4 |
| a |
| 4 |
| a |
由图象可知:
| 4 |
| a |
△CEF的面积是:
| 1 |
| 2 |
| 4 |
| a |
∴△CEF的面积=△DEF的面积,
故①正确;
②△CEF和△DEF以EF为底,则两三角形EF边上的高相等,
故EF∥CD,
∴FE∥AB,
∴△AOB∽△FOE,
故②正确;
③∵C、D是一次函数y=x+3的图象与反比例函数y=
| 4 |
| x |
∴x+3=
| 4 |
| x |
解得:x=-4或x=1,
经检验:x=-4或1都是原分式方程的解,
∴D(1,4),C(-4,-1),
∴DF=4,CE=4,
∵一次函数y=x+3的图象与x轴,y轴交于A,B两点,
∴A(-3,0),B(0,3),
∴∠ABO=∠BAO=45°,
∵DF∥BO,AO∥CE,
∴∠BCE=∠BAO=45°,∠FDA=∠OBA=45°,
∴∠DCE=∠FDA=45°,
在△DCE和△CDF中
|
∴△DCE≌△CDF(SAS),
故③正确;
④∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,
故④正确;
正确的有4个.
故选:C.
点评:本题考查了反比例函数综合题,①利用了自变量与函数值的关系,三角形的面积公式,②利用了等底等高的三角形的面积相等,相似三角形的判定,③利用了函数与方程的关系,平行线的判定,全等三角形的判定,④利用了平行四边形的判定与性质.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )| A、∠B=∠E,BC=EF |
| B、∠A=∠D,BC=EF |
| C、∠A=∠D,∠B=∠E |
| D、BC=EF,AC=DF |
下列结论错误的是( )
| A、0既不是正数,也不是负数 |
| B、两点之间线段最短 |
| C、锐角和钝角互补 |
| D、两点确定一条直线 |
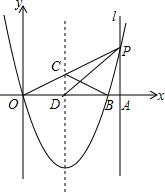 直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.
直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.
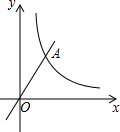 已知图中的曲线是反比例函数y=
已知图中的曲线是反比例函数y=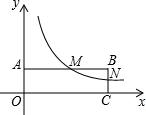 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA、OC为边作矩形OABC,双曲线
如图,在平面直角坐标系中,点A和点C分别在y轴和x轴的正半轴上,以OA、OC为边作矩形OABC,双曲线