题目内容
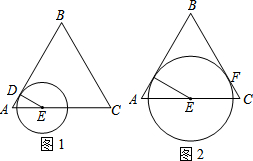 己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒,
己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒,(1)如图1,判断⊙E与AB的位置关系,并证明你的结论;
(2)如图2,当⊙E与BC切于点F时,求t的值.
考点:直线与圆的位置关系
专题:
分析:(1)首先过点D作DM⊥AC于点M,由△ABC为等边三角形,可得∠A=60°,可得AM=
t,DM=
t,继而求得AE与ME的长,则可得在△ADE中,AD2=t2,AE2=4t2,DE2=3t2,证得AD2+DE2=AE2,继而证得AB与⊙D相切;
(2)首先连接BE、EF,由切线长定理可得BE平分∠ABC,然后由等腰三角形的性质,求得AE的长,继而求得答案;
| 1 |
| 2 |
| ||
| 2 |
(2)首先连接BE、EF,由切线长定理可得BE平分∠ABC,然后由等腰三角形的性质,求得AE的长,继而求得答案;
解答: 解:(1)AB与⊙E相切.
解:(1)AB与⊙E相切.
理由如下:过点D作DM⊥AC于点M,
∵△ABC为等边三角形,
∴∠A=60°,
在Rt△ADM中,
∵AD=t,∠A=60°,
∴AM=
t,DM=
t,
∵AE=2t,
∴ME=
t,
在Rt△DME中,DE2=DM2+EM2=3t2,
在△ADE中,∵AD2=t2,AE2=4t2,DE2=3t2,
∴AD2+DE2=AE2,
∴∠ADE=90°,
∴AB与⊙E相切;
(2)连接BE、EF,
∵BD、BF与⊙O相切,
∴BE平分∠ABC,
∵AB=BC,
∴AE=CE,
∵AC=4,
∴AE=2,
∴t=1;
 解:(1)AB与⊙E相切.
解:(1)AB与⊙E相切.理由如下:过点D作DM⊥AC于点M,
∵△ABC为等边三角形,
∴∠A=60°,
在Rt△ADM中,
∵AD=t,∠A=60°,
∴AM=
| 1 |
| 2 |
| ||
| 2 |
∵AE=2t,
∴ME=
| 3 |
| 2 |
在Rt△DME中,DE2=DM2+EM2=3t2,
在△ADE中,∵AD2=t2,AE2=4t2,DE2=3t2,
∴AD2+DE2=AE2,
∴∠ADE=90°,
∴AB与⊙E相切;
(2)连接BE、EF,
∵BD、BF与⊙O相切,
∴BE平分∠ABC,
∵AB=BC,
∴AE=CE,
∵AC=4,
∴AE=2,
∴t=1;
点评:此题考查了切线的性质与判定、勾股定理以及逆定理、圆与圆的位置关系以及切线长定理.此题难度较大,注意掌握辅助线的作法,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
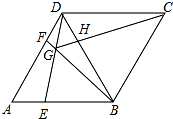 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )| A、只有①② | B、①②③ |
| C、只有②③ | D、只有①③ |
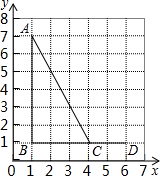 如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,0),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,0),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )| A、(6,0) |
| B、(6,3) |
| C、(6,5) |
| D、(4,2) |
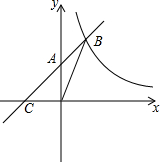
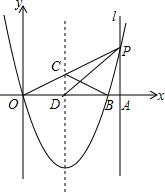 直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.
直线l垂直x轴于点A(4,0),点P是l上的一个动点,经过点P的抛物线y=x2+bx+c与x轴交于原点O和点B,抛物线的对称轴交OP于点C,交x轴于点D,连接PD、PB、BC,设点P的纵坐标为m.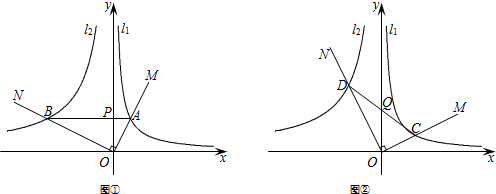
 如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y=
如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y=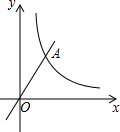 已知图中的曲线是反比例函数y=
已知图中的曲线是反比例函数y= 如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交DC的延长线于点F,AB=2,BE=3EC,那么DF的长为
如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交DC的延长线于点F,AB=2,BE=3EC,那么DF的长为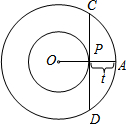 如图,已知OA=4cm,一个动点P从A向O以1cm/秒的速度运动,以O为圆心,分别以OA、OP为半径画大圆和小圆,以P为切点的小圆的切线与大圆交于C、D,则弦CD的长y(cm)关于P的运动时间t(秒)的函数解析式为
如图,已知OA=4cm,一个动点P从A向O以1cm/秒的速度运动,以O为圆心,分别以OA、OP为半径画大圆和小圆,以P为切点的小圆的切线与大圆交于C、D,则弦CD的长y(cm)关于P的运动时间t(秒)的函数解析式为