题目内容
6.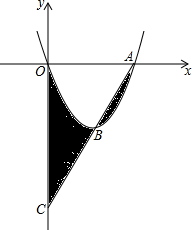 如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )
如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
分析 先通过解方程x2-4x=0得到A(4,0),再把解析式配成顶点式得到B(2,-4),接着利用待定系数法求出直线AB的解析式为y=2x-8,则可得到C(0,-8),然后利用抛物线的对称性得到图中阴影部分的面积和=S△OBC,最后根据三角形面积公式求解.
解答  解:当y=0时,x2-4x=0,解得x1=0,x2=4,则A(4,0),
解:当y=0时,x2-4x=0,解得x1=0,x2=4,则A(4,0),
∵y=x2-4x=(x-2)2-4,
∴B(2,-4),
设直线AB的解析式为y=kx+b,
把A(4,0),B(2,-4)代入得$\left\{\begin{array}{l}{4k+b=0}\\{2k+b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-8}\end{array}\right.$,
∴直线AB的解析式为y=2x-8;
当x=0时,y=2x-8=-8,则C(0,-8),
∴图中阴影部分的面积和=S△OBC=$\frac{1}{2}$×8×2=8.
故选B.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )
如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )
 如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )
如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )| A. | 20 | B. | 16 | C. | 25 | D. | 30 |
1. 如图,在菱形ABCD中,对角线BD=6,∠BAD=60°,则对角线AC的长等于( )
如图,在菱形ABCD中,对角线BD=6,∠BAD=60°,则对角线AC的长等于( )
 如图,在菱形ABCD中,对角线BD=6,∠BAD=60°,则对角线AC的长等于( )
如图,在菱形ABCD中,对角线BD=6,∠BAD=60°,则对角线AC的长等于( )| A. | 12 | B. | $3\sqrt{3}$ | C. | 6 | D. | $6\sqrt{3}$ |
16.若等腰三角形的两边长分别是2和10,则它的周长是( )
| A. | 14 | B. | 22 | C. | 14或22 | D. | 12 |
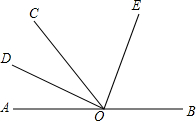 如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,∠AOC=52°,OD平分∠AOC,∠DOE=90°.