题目内容
18.某市计划进行一项城市美化工程,已知乙队单独完成此项工程比甲队单独完成此项工程多用10天,且甲队单独施工30天和乙队单独施工45天的工作量相同.(1)甲、乙两队单独完成此项工程各需多少天?
(2)已知甲队每天的施工费用为8000元,乙队每天的施工费用为6000元,为了缩短工期,指挥部决定该工程由甲、乙两队一起来完成,则该工程施工费用是多少元?
分析 (1)设甲队单独完成此项任务需要x天,则乙队单独完成此项任务需要(x+10)天,根据甲队单独施工30天和乙队单独施工45天的工作量相同建立方程求出其解即可;
(2)根据(1)中的结论求得甲乙合作的天数为12天,利用总费用=(甲队每天的施工费用+乙队每天的施工费用)×12进行解答.
解答 解:(1)设甲单独完成需x天,根据题意得:
$\frac{30}{x}$=$\frac{45}{x+10}$,
解得:x=20,
经检验x=20是原方程的解,
所以x+10=30,
答:甲单独完成需20天,乙单独完成需30天;
(2)甲乙合作的天数:1÷($\frac{1}{20}$+$\frac{1}{30}$)=12(天),
总费用为:(8000+6000)×12=168000(元).
答:该工程施工费用是168000元.
点评 本题考查分式方程的应用,利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
13.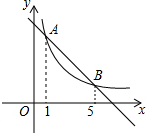 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )| A. | -5<x<-1或x>0 | B. | 0<x<1或x>5 | C. | 1<x<5 | D. | -5<x<-1 |
3.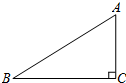 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )| A. | $\frac{{\sqrt{7}}}{3}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
7.点M(x,y)在第二象限内,且|x|=2,|y|=3,则点M关于x轴的对称点的坐标是( )
| A. | (2,3) | B. | (-2,-3) | C. | (-3,2) | D. | (-3,-2) |
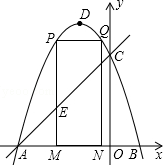 如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.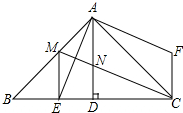 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.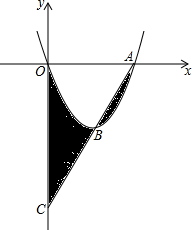 如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )
如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( ) 如图,转盘中8个扇形的面积都相等,任意转动转盘1次.当转盘停止转动时,指针指向大于5的数的概率为$\frac{3}{8}$.
如图,转盘中8个扇形的面积都相等,任意转动转盘1次.当转盘停止转动时,指针指向大于5的数的概率为$\frac{3}{8}$.