题目内容
11.如图1,直线y=2x-2与曲线y=$\frac{m}{x}$(x>0)相交于点A(2,n),与x轴、y轴分别交于点B、C.(1)求曲线的解析式;
(2)试求AB•AC的值?
(3)如图2,点E是y轴正半轴上一动点,过点E作直线AC的平行线,分别交x轴于点F,交曲线于点D.是否存在一个常数k,始终满足:DE•DF=k?如果存在,请求出这个常数k;如果不存在,请说明理由.
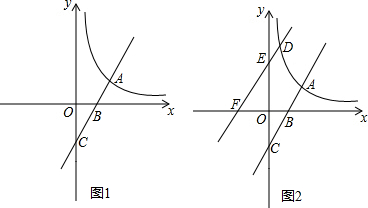
分析 (1)首先把A代入直线解析式求得A的坐标,然后利用待定系数法求得反比例函数解析式;
(2)首先求得A和B的坐标,过A作AM⊥x轴于点M,然后利用勾股定理求得AB和BC的长,则AB和AC的长即可求得,则两线段的乘积即可求得;
(3)过点D作DN⊥x轴于点N.过点E作EG⊥DN于点G,易证△ABM∽△DFN,△ABM∽△DEG,根据相似三角形的对应边的比相等即可求解.
解答 解:(1)∵直线y=2x-2经过点A(2,n),
∴n=2×2-2=2,即A的坐标是(2,2),
把(2,2)代入y=$\frac{m}{x}$得m=4,
则反比例函数的解析式是y=$\frac{4}{x}$(x>0);
(2)过A作AM⊥x轴于点M.
在y=2x-2中,令x=0解得y=-2,则C的坐标是(0,-2),令y=0,则2x-2=0,解得x=1,则B的坐标是(1,0);
则AB=$\sqrt{A{M}^{2}+B{M}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
则AB•AC=$\sqrt{5}$×2$\sqrt{5}$=10;
(3)存在常数k,过点D作DN⊥x轴于点N.过点E作EG⊥DN于点G,则∠AMB=∠DNF=∠DGE=90°,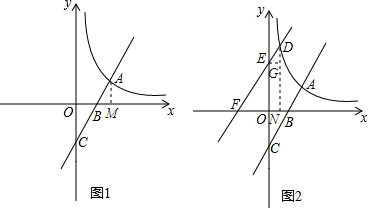
设D的坐标是(a,$\frac{4}{m}$),则EG=a,DN=$\frac{4}{m}$,
∵DF∥AC,EG∥FN,
∴∠ABM=∠DFG=∠DEG,
∴△ABM∽△DFN,△ABM∽△DEG,
∴$\frac{DF}{DN}$=$\frac{AB}{AM}$,有DF:$\frac{4}{a}$=$\frac{\sqrt{5}}{2}$,则DF=2$\sqrt{5}$a,
又$\frac{AB}{BM}$=$\frac{ED}{EG}$,有$\frac{\sqrt{5}}{1}$=$\frac{EG}{a}$,则ED=$\sqrt{5}$a,
于是,DE•DF=$\sqrt{5}$a•$\frac{2\sqrt{5}}{a}$=10.
即存在常数k=10.
点评 本题考查了待定系数法求函数解析式以及相似三角形的判定与性质,正确作出辅助线,构造相似三角形是关键.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
(1)观察图形,填写下表:
| 图形 | (1) | (2) | (3) |
| 正方形的个数 | 2 | 5 | 9 |
| 图形的周长 | 8 | 12 | 16 |
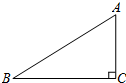 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )| A. | $\frac{{\sqrt{7}}}{3}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 2 | B. | -3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
 如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.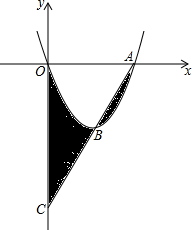 如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )
如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( ) 如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )
如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )