题目内容
16.若等腰三角形的两边长分别是2和10,则它的周长是( )| A. | 14 | B. | 22 | C. | 14或22 | D. | 12 |
分析 本题没有明确已知的两边的具体名称,要分为两种情况即:①2为底,10为腰;②10为底,2为腰,可求出周长.注意:必须考虑三角形的三边关系进行验证能否组成三角形.
解答 解:∵等腰三角形的两边分别是2和10,
∴应分为两种情况:①2为底,10为腰,则2+10+10=22;
②10为底,2腰,而2+2<10,应舍去,
∴三角形的周长是22.
故选B.
点评 本题考查了等腰三角形的性质及三角形三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.点M(x,y)在第二象限内,且|x|=2,|y|=3,则点M关于x轴的对称点的坐标是( )
| A. | (2,3) | B. | (-2,-3) | C. | (-3,2) | D. | (-3,-2) |
11.一个正多边形的每个外角都是72°,这个正多边形的边数是( )
| A. | 9 | B. | 10 | C. | 6 | D. | 5 |
1.下列各数中,最小的数是( )
| A. | 2 | B. | -3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
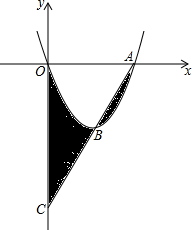 如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )
如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( ) 如图,在△ABC中,BE⊥AC,CF⊥AB,BE与CF相交于点D,且BD=AC,点G在CF的延长线上,且CG=AB.
如图,在△ABC中,BE⊥AC,CF⊥AB,BE与CF相交于点D,且BD=AC,点G在CF的延长线上,且CG=AB. 如图,转盘中8个扇形的面积都相等,任意转动转盘1次.当转盘停止转动时,指针指向大于5的数的概率为$\frac{3}{8}$.
如图,转盘中8个扇形的面积都相等,任意转动转盘1次.当转盘停止转动时,指针指向大于5的数的概率为$\frac{3}{8}$.