题目内容
14. 如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )
如图,在菱形ABCD中,BD=6,AC=8,则菱形ABCD的周长为( )| A. | 20 | B. | 16 | C. | 25 | D. | 30 |
分析 根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOB中,根据勾股定理可以求得AB的长,即可求菱形ABCD的周长.
解答 解:∵在菱形ABCD中,BD=6,AC=8,
∴BO=OD=3,AO=OC=4,AC⊥BD,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∴菱形ABCD的周长=5×4=20.
故选A.
点评 本题考查了菱形各边长相等的性质,勾股定理在直角三角形中的运用,本题中根据勾股定理计算AB的长是解题的关键.

练习册系列答案
相关题目
2.观察与探究:

(1)观察图形,填写下表:
(2)推测第n个图形中,正方形的个数为$\frac{{n}^{2}+n}{2}$,周长为4n+4.

(1)观察图形,填写下表:
| 图形 | (1) | (2) | (3) |
| 正方形的个数 | 2 | 5 | 9 |
| 图形的周长 | 8 | 12 | 16 |
3.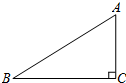 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
 如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AB=4,则cosB的值是( )| A. | $\frac{{\sqrt{7}}}{3}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
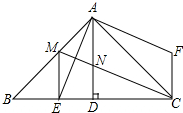 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC. 如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.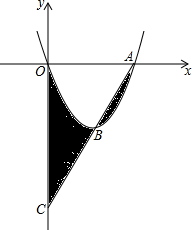 如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )
如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( ) 如图,在△ABC中,BE⊥AC,CF⊥AB,BE与CF相交于点D,且BD=AC,点G在CF的延长线上,且CG=AB.
如图,在△ABC中,BE⊥AC,CF⊥AB,BE与CF相交于点D,且BD=AC,点G在CF的延长线上,且CG=AB.