题目内容
1. 如图,在菱形ABCD中,对角线BD=6,∠BAD=60°,则对角线AC的长等于( )
如图,在菱形ABCD中,对角线BD=6,∠BAD=60°,则对角线AC的长等于( )| A. | 12 | B. | $3\sqrt{3}$ | C. | 6 | D. | $6\sqrt{3}$ |
分析 由四边形ABCD为菱形,得到四条边相等,对角线垂直且互相平分,根据∠BAD=60°得到三角形ABD为等边三角形,在直角三角形ABO中,利用勾股定理求出OA的长,即可确定出AC的长.
解答 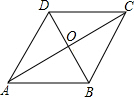 解:设对角线AC与BD交于点O.
解:设对角线AC与BD交于点O.
∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD,
∵∠BAD=60°,
∴△ABD为等边三角形,
∴BD=AB=6,OD=OB=3,
在Rt△AOB中,根据勾股定理得:OA=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
则AC=2OA=6$\sqrt{3}$,
故选D.
点评 此题考查了菱形的性质,勾股定理,以及等边三角形的判定与性质,熟练掌握菱形的性质是解本题的关键.

练习册系列答案
相关题目
20.生产厂家检测4个足球的质量,结果如图所示,超过标准质量的克数记为正数,不足标准质量的克数记为负数,其中最接近标准质量的足球是( )
| A. |  -3.5 | B. |  -0.6 | C. |  +0.7 | D. |  +2.5 |
16.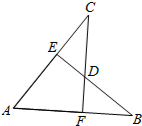 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.
 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.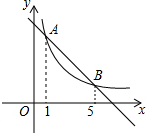 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )| A. | -5<x<-1或x>0 | B. | 0<x<1或x>5 | C. | 1<x<5 | D. | -5<x<-1 |
11.一个正多边形的每个外角都是72°,这个正多边形的边数是( )
| A. | 9 | B. | 10 | C. | 6 | D. | 5 |
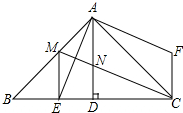 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.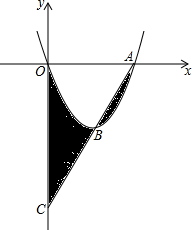 如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )
如图,抛物线y=x2-4x与x轴交于点O、A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )