题目内容
8.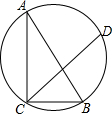 如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).
如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).
分析 连接OD,要求$\widehat{BD}$的长度,只需求出圆的半径和$\widehat{BD}$所对圆心角的度数即可.
解答 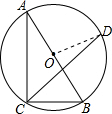 解:连接OD,如图.
解:连接OD,如图.
∵∠ACB=90°,∠A=30°,BC=3,
∴AB是⊙O的直径,AB=2BC=6,
∴OB=3.
∵∠BCD=40°,
∴∠BOD=80°,
∴$\widehat{BD}$的长度为$\frac{80π×3}{180}$=$\frac{4π}{3}$.
故答案为$\frac{4π}{3}$.
点评 本题主要考查了圆周角定理、30°角所对的直角边等于斜边的一半、圆弧长公式等知识,其中圆弧长公式为l=$\frac{nπr}{180}$.

练习册系列答案
相关题目
3.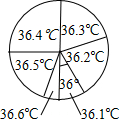 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
 为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )| 体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
| 人数(人) | 4 | 8 | 8 | 10 | x | 2 |
| A. | 这些体温的众数是8 | B. | 这些体温的中位数是36.35 | ||
| C. | 这个班有40名学生 | D. | x=8 |
13.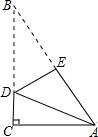 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
 如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为H,AD的中点E的对应点记为G,若△GFH∽△GBF,则AD=$\frac{16}{5}$.
如图,直角三角形ABC中,∠ACB=90°,AB=10,BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为H,AD的中点E的对应点记为G,若△GFH∽△GBF,则AD=$\frac{16}{5}$.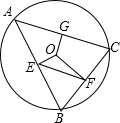 如图,⊙O的半径是$\sqrt{5}$,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为2.
如图,⊙O的半径是$\sqrt{5}$,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为2.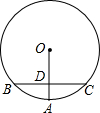 如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.
如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.