题目内容
3．
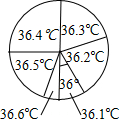为了解九（1）班学生的体温情况，对这个班所有学生测量了一次体温（单位：℃），小明将测量结果绘制成如下统计表和如图所示的扇形统计图．下列说法错误的是（ ）| 体温（℃） | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
| 人数（人） | 4 | 8 | 8 | 10 | x | 2 |
| A． | 这些体温的众数是8 | B． | 这些体温的中位数是36.35 | ||
| C． | 这个班有40名学生 | D． | x=8 |
分析 根据扇形统计图可知：36.1°C所在扇形的圆心角为36°，由此可得到36.1℃在总体中所占的百分比，再结合36.1℃的频数，就可求出九（1）班学生总数，进而可求出x的值，然后根据众数和中位数的定义就可解决问题．
解答 解：由扇形统计图可知：体温为36.1℃所占的百分数为$\frac{36}{360}$×100%=10%，
则九（1）班学生总数为$\frac{4}{10%}$=40，故C正确；
则x=40-（4+8+8+10+2）=8，故D正确；
由表可知这些体温的众数是36.4℃，故A错误；
由表可知这些体温的中位数是$\frac{36.3+36.4}{2}$=36.35（℃），故B正确．
故选A．
点评 本题主要考查了表格与扇形统计图、众数及中位数的定义、圆心角的度数与项目所占百分比的关系、频数、总数及频率的关系等知识，利用36.1℃的频数及在总体中所占的百分比，是解决本题的关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
13．
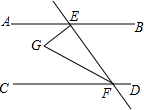如图，AB∥CD，EF与AB，CD分别交于点E，F，EG⊥EF，与∠EFC的平分线FG交于点G．若∠EFG=25°，则∠AEG的大小为（ ）
如图，AB∥CD，EF与AB，CD分别交于点E，F，EG⊥EF，与∠EFC的平分线FG交于点G．若∠EFG=25°，则∠AEG的大小为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
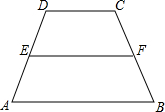如图，在梯形△ABCD中，E、F分别为腰AD、BC的中点，若$\overrightarrow{DC}$=$3\overrightarrow m$，$\overrightarrow{EF}$=$5\overrightarrow m$，则向量$\overrightarrow{AB}$=7$\overline m$（结果用$\overrightarrow m$表示）．
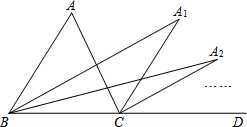如图，∠ACD是△ABC的外角，∠ABC的平分线与∠ACD的平分线交于点A1，∠A1BC的平分线与∠A1CD的平分线交于点A2，…∠An-1BC的平行线与∠An-1CD的平分线交于点An，设∠A=θ，则∠An=$\frac{θ}{{2}^{n}}$．
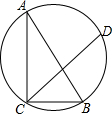如图，一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上，已知弦CD与CB的夹角∠BCD=40°，BC=3，则$\widehat{BD}$的长度为$\frac{4π}{3}$（结果保留π）．
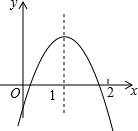二次函数y=ax2+bx+c的图象如图所示，下列结论：