题目内容
20.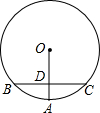 如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.
如图,OA是⊙O的半径,BC是⊙O的弦,OA⊥BC,垂足为D点,如果OD=3,DA=2,那么BC=8.
分析 连接OB,求出OB,根据垂径定理求出BC=2BD,根据勾股定理求出BD即可.
解答 解:如图,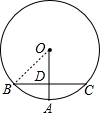
连接OB,
∵OA⊥BC,OA过O,
∴BC=2BD,∠ODB=90°,
∵OD=3,DA=2,
∴OA=2+3=5,
∴OB=OA=5,
在Rt△ODB中,由勾股定理得:BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴BC=2BD=8,
故答案为:8.
点评 本题考查了垂径定理和勾股定理的应用,能根据垂径定理得出BC=2BD是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5. 将图中所示的图案平移后得到的图案是( )
将图中所示的图案平移后得到的图案是( )
 将图中所示的图案平移后得到的图案是( )
将图中所示的图案平移后得到的图案是( )| A. |  | B. |  | C. |  | D. |  |
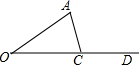 如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为60°或90°°.
如图,已知∠AOD=30°,点C是射线OD上的一个动点.在点C的运动过程中,△AOC恰好是直角三角形,则此时∠A所有可能的度数为60°或90°°.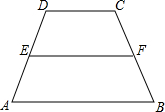 如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).
如图,在梯形△ABCD中,E、F分别为腰AD、BC的中点,若$\overrightarrow{DC}$=$3\overrightarrow m$,$\overrightarrow{EF}$=$5\overrightarrow m$,则向量$\overrightarrow{AB}$=7$\overline m$(结果用$\overrightarrow m$表示).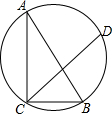 如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).
如图,一块含30°角的直角三角形ABC的三个顶点刚好都在一个圆上,已知弦CD与CB的夹角∠BCD=40°,BC=3,则$\widehat{BD}$的长度为$\frac{4π}{3}$(结果保留π).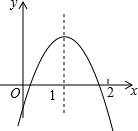 二次函数y=ax2+bx+c的图象如图所示,下列结论:
二次函数y=ax2+bx+c的图象如图所示,下列结论: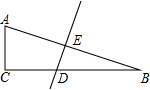 如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线分别交AB、BC于点E和点D,已知BD:CD=2:$\sqrt{3}$.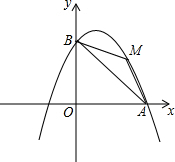 如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.
如图,以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数)经过A(4,0)和B(0,4)两点,其顶点为C.