题目内容
13.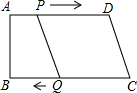 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.(1)从运动开始,经过多少时间点P、Q、C、D为边得四边形是平行四边形?
(2)从运动开始,经过多少时间点A、B、Q、P为边得四边形是矩形?
分析 (1)根据对边平行且相等的四边形是平行四边形列出方程,解方程即可;
(2)由AD∥BC,∠B=90°,可得当AP=BQ时,四边形ABQP是矩形,即可得方程:t=26-2t,解此方程即可求得答案.
解答 解:(1)当PD=CQ时,四边形PQCD为平行四边形,
即24-t=3t,
解得,t=6,
即当t=6s时,四边形PQCD为平行四边形;
(2)根据题意得:AP=tcm,CQ=3tcm,
∵AB=8cm,AD=24cm,BC=26cm,
∴DP=AD-AP=24-t(cm),BQ=26-3t(cm),
∵AD∥BC,∠B=90°,
∴当AP=BQ时,四边形ABQP是矩形,
∴t=26-3t,
解得:t=6.5,
即当t=6.5s时,四边形ABQP是矩形;
点评 此题考查了直角梯形的性质、平行四边形的判定、矩形的判定形的判定.熟练掌握平行四边形和矩形的判定,根据题意得出方程是解决问题的关键.

练习册系列答案
相关题目
12.为了配合“交通安全”宣传教育,针对闯红灯的现象时有发生的实际情况,九年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早、中、晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志.数据汇总如下:
部分时段车流量情况调查表
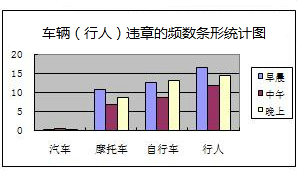 回答下列问题:
回答下列问题:
(1)请你写出2条交通法规:①红灯停、绿灯行,②过马路要走人行横道线;
(2)早晨、中午、晚上三个时段每分钟车流量的极差是74,这三个时段的车流总量的中位数是2747;
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因;
(4)通过分析写一条合理化建议.
部分时段车流量情况调查表
| 时间 | 负责组别 | 车流总量 | 每分钟车流量 |
| 早晨上学6:30~7:00 | ①② | 2747 | 92 |
| 中午放学11:20~11:50 | ③④ | 1449 | 48 |
| 下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
 回答下列问题:
回答下列问题:(1)请你写出2条交通法规:①红灯停、绿灯行,②过马路要走人行横道线;
(2)早晨、中午、晚上三个时段每分钟车流量的极差是74,这三个时段的车流总量的中位数是2747;
(3)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因;
(4)通过分析写一条合理化建议.
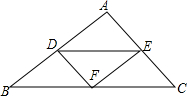 如图,△ABC是由四个形状、大小完全一样的三角形拼成,则可以看着是由△ADE平移得到的小三角形是△DBF或△EFC.
如图,△ABC是由四个形状、大小完全一样的三角形拼成,则可以看着是由△ADE平移得到的小三角形是△DBF或△EFC.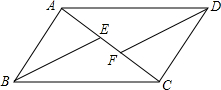 已知?ABCD中,AC是对角线,BE平分∠ABC交AC于点E,DF平分∠ADC交AC于点F,求证:AE=CF.
已知?ABCD中,AC是对角线,BE平分∠ABC交AC于点E,DF平分∠ADC交AC于点F,求证:AE=CF.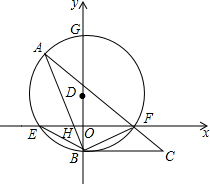 如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.
如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.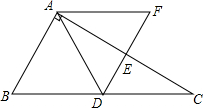 如图,Rt△ABC中,∠BAC=90°,∠C=30°.点D、E分别是边BC、AC的中点,DE的联线与BC的平行线AF交于点F.
如图,Rt△ABC中,∠BAC=90°,∠C=30°.点D、E分别是边BC、AC的中点,DE的联线与BC的平行线AF交于点F.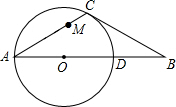 如图,在△ABC中,CA=CB,∠CAB=30°,⊙O经过点C,且圆的直径AD在线段AB上.
如图,在△ABC中,CA=CB,∠CAB=30°,⊙O经过点C,且圆的直径AD在线段AB上.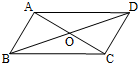 如图,在?ABCD中,AC=6,BD=10,
如图,在?ABCD中,AC=6,BD=10,