题目内容
4.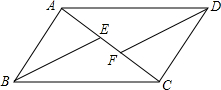 已知?ABCD中,AC是对角线,BE平分∠ABC交AC于点E,DF平分∠ADC交AC于点F,求证:AE=CF.
已知?ABCD中,AC是对角线,BE平分∠ABC交AC于点E,DF平分∠ADC交AC于点F,求证:AE=CF.
分析 先根据平行四边形的性质得出∠ABC=∠CDA,然后利用角平分线的知识证明∠BAE=∠DCF,从而根据三角形全等的判定定理即可作出证明.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∠ABC=∠CDA,
∵BE平分∠ABC,DF平分∠ADC,
∴∠ABE=∠CDF,
∵AB∥CD,
∴∠BAE=∠DCF
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠ABE=∠CDF}\\{AB=CD}\\{∠BAE=∠DCF}\end{array}\right.$,
∴△ABE≌△CDF(ASA),
∴AE=CF.
点评 本题考查了平行四边形的性质,全等三角形的判定和性质,解答本题的关键寻找两三角形全等所需要的条件,然后根据三角形全等的判定定理进行证明.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
19. 如图,在?ABCD中,下列结论一定正确的是( )
如图,在?ABCD中,下列结论一定正确的是( )
 如图,在?ABCD中,下列结论一定正确的是( )
如图,在?ABCD中,下列结论一定正确的是( )| A. | AC⊥BD | B. | AC=BD | C. | AB=AD | D. | AO=CO |
16.下列方程组中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{2x-5y=8}\\{x=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x=y+z}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-3y=2}\\{2x+y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{3}y=2}\\{\frac{1}{3}x-\frac{1}{2}y=3}\end{array}\right.$ |
14.不等式$-\frac{1}{2}≤\frac{1-0.6x}{-3}≤\frac{2}{3}$的整数解的个数为( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
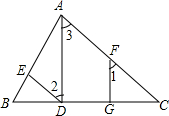 已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,求证∠BDE=∠C.
已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,求证∠BDE=∠C.
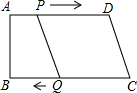 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.