题目内容
8.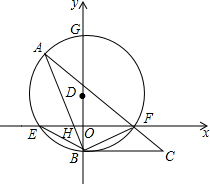 如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.
如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH•AB;
(3)若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
分析 (1)首先连接GF,由BG是⊙D直径,可得∠GFB=90°,然后由圆周角定理,求得∠FBC+∠GBF=90°,继而证得结论;
(2)首先连接AE,由垂径定理可得$\widehat{BE}$=$\widehat{BF}$,继而证得△BEH∽△BAE,然后由相似三角形的对应边成比例,证得结论;
(3)首先过点A作AQ⊥GB于点Q,由垂径定理即可求得OE与OF的长,然后由勾股定理求得BH的长,再利用△BOH∽△BQA,求得答案.
解答  解:(1)直线BC与⊙D相切.
解:(1)直线BC与⊙D相切.
证明:如图,连接GF,
∵BG是⊙D直径,
∴∠GFB=90°,
∴∠BGF+∠GBF=90°,
∵∠BAF=∠BGF,∠FBC=∠A,
∴∠BGF=∠FBC,
∴∠FBC+∠GBF=90°,
即∠GBC=90°,
∴直线BC与⊙D相切;
(2)如图,连接AE,
∵BG⊥EF,BG是⊙D直径,
∴$\widehat{BE}$=$\widehat{BF}$,
∴∠BEH=∠BAE,
∵∠BAE=∠EAH,
∴△BEH∽△BAE,
∴$\frac{BE}{BH}$=$\frac{AB}{BE}$,
∴BE2=BH•AB;
(3)过点A作AQ⊥GB于点Q,
∵E(-4,0),根据垂径定理得OE=OF=4,
∴F(4,0),
∵BE2=BH•AB,BE2=OE2+OB2=16+4=20,AB=8,
∴BH=2.5,
得OH=1.5,
由△BOH∽△BQA得:$\frac{BO}{BQ}=\frac{OH}{AQ}=\frac{BH}{BA}$,
∴AQ=4.8,BQ=6.4,
∴OQ=4.4,
∴A(-4.8,4.4)或(4.8,4.4)
点评 此题属于圆的综合题.考查了切线的判定与性质、圆周角定理、垂径定理以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案 如图,在?ABCD中,下列结论一定正确的是( )
如图,在?ABCD中,下列结论一定正确的是( )| A. | AC⊥BD | B. | AC=BD | C. | AB=AD | D. | AO=CO |
| A. | $\left\{\begin{array}{l}{2x-5y=8}\\{x=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x=y+z}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-3y=2}\\{2x+y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{3}y=2}\\{\frac{1}{3}x-\frac{1}{2}y=3}\end{array}\right.$ |
| A. | 一个角是直角 | B. | 对角线相等 | C. | 一组邻角相等 | D. | 对角线互相垂直 |

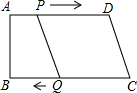 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.