题目内容

18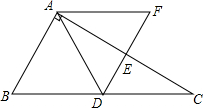．如图，Rt△ABC中，∠BAC=90°，∠C=30°．点D、E分别是边BC、AC的中点，DE的联线与BC的平行线AF交于点F．
求证：四边形ABDF是菱形．

分析 先证明四边形ABDF是平行四边形，再证明邻边AB=BD即可．

解答 证明：∵AE=EC，BD=DC，
∴DE∥AB，
∵AF∥BC，
∴四边形ABDF是平行四边形，
∵∠BAC=90°，BD=DC，∠C=30°
∴AB=$\frac{1}{2}$BC=BD，
∵四边形ABDF是平行四边形，又∵BA=BD，
∴四边形ABDF是菱形．

点评 本题考查菱形的判定，记住菱形的判定方法①邻边相等的平行四边形是菱形，②四边相等的四边形是菱形，③对角线垂直的平行四边形是菱形，属于中考常考题型．

练习册系列答案
相关题目
8．已知正六边形ABCDEF的边心距为$\sqrt{3}$cm，则正六边形的半径为（　　）cm．
A．2$\sqrt{3}$B．2C．$\sqrt{3}$D．4
9．如图1所示，一张三角形纸片ABC，∠ACB=90°，AC=8，BC=6，沿斜边AB的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形（如图2所示）．将纸片△AC1D1沿直线D2B（A→B方向）平移（点A，D1，D2，B始终在同一直线上），当D1与点B重合时，停止平移．在平移的过程中，C1D1与BC2交于点E，AC1与C2D2、BC2分别交于点F、P．
（1）当△AC1D1平移到如图3所示位置时，猜想D1E与D2F的数量关系，并说明理由．
（2）设平移距离D2D1为x，△AC1D1和△BC2D2重复部分面积为y，请写出y与x的函数关系式，以及自变量的取值范围；
（3）对于（2）中的结论是否存在这样的x，使得重复部分面积等于原△ABC纸片面积的$\frac{3}{8}$？若存在，请求出x的值；若不存在，请说明理由．
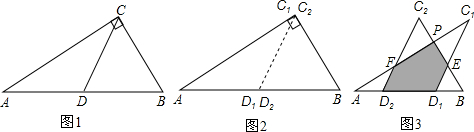
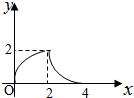
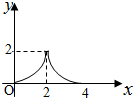
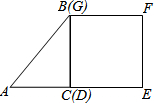6．如图，等腰Rt△ABC（∠ACB=90°）的直角边与正方形DEFG的边长均为2，且AC与DE在同一条直线上，开始时点C与点D重合．将△ABC沿直线DE向右平移，直到点A与点E重合为止．设CD的长为x，若△ABC与正方形DEFG重合部分的面积为y，则y与x的函数图象是（　　）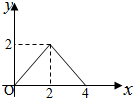
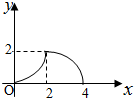
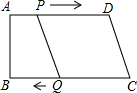A．B．C．D．
13．如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，点P从A点出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．
（1）从运动开始，经过多少时间点P、Q、C、D为边得四边形是平行四边形？
（2）从运动开始，经过多少时间点A、B、Q、P为边得四边形是矩形？
3．下列各式从左到右，不是因式分解的是（　　）
A．x2+xy+1=x（x+y）+1B．a2-b2=（a+b）（a-b）
C．x2-4xy+4y2=（x-2y）2D．ma+mb+mc=m（a+b+c）
10．已知平行四边形ABCD中，∠A=2∠B，则∠C=（　　）
A．30°B．60°C．90°D．120°
7．如图，平面直角坐标系中，O为菱形ABCD的对称中心，已知C（2，0），D（0，-1），N为线段CD上一点（不与C、D重合）．
（1）求以C为顶点，且经过点D的抛物线解析式；
（2）设N关于BD的对称点为N1，N关于BC的对称点为N2，求证：△N1BN2∽△ABC；
（3）求（2）中N1N2的最小值；
（4）过点N作y轴的平行线交（1）中的抛物线于点P，点Q为直线AB上的一个动点，且∠PQA=∠BAC，求当PQ最小时点Q坐标．
17．如图，在△ABC中，BE⊥AC于点E，AD⊥BC于点D，连接DE．
（1）如图1，若AD=3，AB=BC=5，求ED的长；
（2）如图2，若∠ABC=45°，求证：CE+EF=$\sqrt{2}$ED；
（3）如图3，若∠ABC=45°，现将△ADC沿AC边翻折得到△AGC，连接EG、DG．猜想线段AE、DG、BE之间的数量关系，写出关系式，并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网