题目内容
2.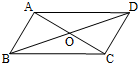 如图,在?ABCD中,AC=6,BD=10,
如图,在?ABCD中,AC=6,BD=10,(1)设?ABCD的边BC=x,则x的取值范围是2<x<8;
(2)若AC⊥AB,则?ABCD的周长等于8+4$\sqrt{13}$.
分析 (1)根据平行四边形两条对角线互相平分可得CO=$\frac{1}{2}$AC=3,BO=$\frac{1}{2}$BD=5,再根据三角形的三边关系可得5-3<x<5+3,进而可得x的取值范围.
(2)首先利用勾股定理在直角△ABO中计算出AB的长,再次利用勾股定理计算出BC的长,进而可得周长.
解答 解:(1)∵四边形ABCD是平行四边形,
∴CO=$\frac{1}{2}$AC=3,BO=$\frac{1}{2}$BD=5,
∴5-3<x<5+3,
∴2<x<8,
故答案为:2<x<8;
(2)∵在?ABCD中,AC=6,BD=10,
∴AO=CO=3,BO=DO=5,
∵AC⊥AB,
∴AB=$\sqrt{B{O}^{2}-A{O}^{2}}$=4,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=2$\sqrt{13}$,
∴?ABCD的周长等于:2(4+2$\sqrt{13}$)=8+4$\sqrt{13}$.
故答案为:8+4$\sqrt{13}$.
点评 此题主要考查了平行四边形的性质,以及勾股定理的应用,关键是掌握平行四边形两条对角线互相平分,平行四边形的对边相等.

练习册系列答案
相关题目
10.已知平行四边形ABCD中,∠A=2∠B,则∠C=( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
14.不等式$-\frac{1}{2}≤\frac{1-0.6x}{-3}≤\frac{2}{3}$的整数解的个数为( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
11.使分式$\frac{x+3}{2x-8}$有意义的x值是( )
| A. | x=4 | B. | x=-3 | C. | x≠4 | D. | x=≠-3 |
1.下列各实数中,无理数是( )
| A. | $\sqrt{4}$ | B. | 0 | C. | $\root{3}{9}$ | D. | ($\sqrt{2}$)0 |
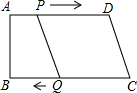 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.