题目内容
5.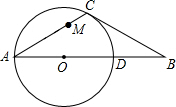 如图,在△ABC中,CA=CB,∠CAB=30°,⊙O经过点C,且圆的直径AD在线段AB上.
如图,在△ABC中,CA=CB,∠CAB=30°,⊙O经过点C,且圆的直径AD在线段AB上.(1)试说明CB是⊙O的切线;
(2)∠AOC的平分线OE交弧AC于点E,求证:四边形AOCE是菱形;
(3)在(2)的条件下,设点M是线段AC上任意一点(不含端点),连接OM,当$\frac{1}{2}$CM+OM的最小值为4$\sqrt{3}$时,求⊙O的半径r的值.
分析 (1)首先连接OC,由在△ABC中,CA=CB,∠CAB=30°,易得∠ACB=120°,∠ACO=30°,继而证得结论;
(2)由∠CAB=30°,易证得△AOE和△COE是等边三角形,即可得AO=OC=CE=EA,继而证得四边形AOCE是菱形;
(3)首先由(2)易得O、E两点关于AC对称,然后连接MO,ME,则MO=ME,过M点作MF⊥OC,垂足为F,可得当当E、M、F三点共线时,$\frac{1}{2}$CM+OM有最小值,继而求得答案.
解答 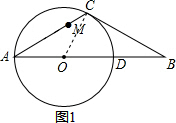 (1)证明:如图1,连接OC,
(1)证明:如图1,连接OC,
∵OA=OC,
∴∠OCA=∠OAC=30°,
又∵CA=CB,∠CAB=30°,
∴∠ACB=120°,
∴∠OCB=∠ACB-∠OCA=120°-30°=90°,
∴CB⊥CO,
即CB是⊙O的切线;
(2)证明:∵OA=OC,∠CAB=30°,
∴∠AOC=120°,
又∵OE平分∠AOC,
∴∠AOE=∠COE=60°,
又∵OA=OE=OC,
∴△AOE和△COE都是等边三角形,
∴AO=OC=CE=EA
∴四边形AOCE是菱形;
(3)解:由(2)知:四边形AOCE是菱形,
∴OE与AC互相垂直且平分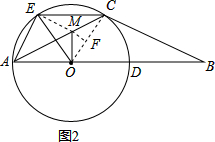 ,
,
∴O、E两点关于AC对称,
连接MO,ME,则MO=ME,
过M点作MF⊥OC,垂足为F,
在Rt△MFC中,∠MCF=30°,
∴MF=$\frac{1}{2}$CM,
∴$\frac{1}{2}$CM+OM=MF+ME≥EF,
即当E、M、F三点共线时,$\frac{1}{2}$CM+OM有最小值,最小值是EF=4$\sqrt{3}$,
在Rt△OEF中,EF=OEsin∠EOF,
即4$\sqrt{3}$=r•$\frac{\sqrt{3}}{2}$,
∴r=8.
点评 此题属于圆的综合题.考查了切线的判定与性质、等腰三角形的性质、等边三角形的判定与性质、菱形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | $\left\{\begin{array}{l}{2x-5y=8}\\{x=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{x=y+z}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-3y=2}\\{2x+y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{2}x+\frac{1}{3}y=2}\\{\frac{1}{3}x-\frac{1}{2}y=3}\end{array}\right.$ |
| A. | 一个角是直角 | B. | 对角线相等 | C. | 一组邻角相等 | D. | 对角线互相垂直 |
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
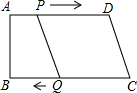 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,点P从A点出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动.
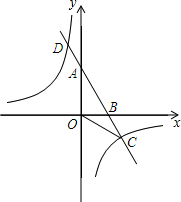 如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a).
如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a).