题目内容
 如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.考点:垂径定理的应用,勾股定理
专题:
分析:连接ON,OB,通过求距离水面2米高处即HD长为2时,桥有多宽即MN的长与货船顶部的3米做比较来判定货船能否通过(MN大于3则能通过,MN小于等于3则不能通过).先根据半弦,半径和弦心距构造直角三角形求出半径的长,再根据Rt△OHN中勾股定理求出HN的长,从而求得MN的长
解答: 解:如图,连接ON,OB.
解:如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=7.2m,
∴BD=
AB=3.6m.
又∵CD=2.4m,
设OB=OC=ON=r,则OD=(r-2.4)m.
在Rt△BOD中,根据勾股定理得:r2=(r-2.4)2+3.62,
解得r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面2m,
∴CH=2.4-2=0.4m,
∴OH=r-CH=3.9-0.4=3.5m,
在Rt△OEN中,HN2=ON2-OH2=3.92-3.52=2.96(m2),
∴EN=
(m).
∴MN=2HN=2×
≈3.44m>3m.
∴此货船能顺利通过这座拱桥.
 解:如图,连接ON,OB.
解:如图,连接ON,OB.∵OC⊥AB,
∴D为AB中点,
∵AB=7.2m,
∴BD=
| 1 |
| 2 |
又∵CD=2.4m,
设OB=OC=ON=r,则OD=(r-2.4)m.
在Rt△BOD中,根据勾股定理得:r2=(r-2.4)2+3.62,
解得r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面2m,
∴CH=2.4-2=0.4m,
∴OH=r-CH=3.9-0.4=3.5m,
在Rt△OEN中,HN2=ON2-OH2=3.92-3.52=2.96(m2),
∴EN=
| 2.96 |
∴MN=2HN=2×
| 2.96 |
∴此货船能顺利通过这座拱桥.
点评:考查了垂径定理的应用,解决此类桥拱问题,通常是利用半弦,半径和弦心距构造直角三角形,根据直角三角形中的勾股定理作为相等关系解方程求线段的长度.要注意本题是通过求距离水面2米高处即HD长为2时,桥有多宽即MN的长与货船顶部的3米做比较来判定货船能否通过(MN大于3则能通过,MN小于等于3则不能通过).

练习册系列答案
相关题目
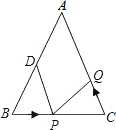 如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动. 如图,AB=AC,AD是∠EAC的平分线,AD∥BC,∠B=64°,求∠EAD、∠DAC、∠C的度数.
如图,AB=AC,AD是∠EAC的平分线,AD∥BC,∠B=64°,求∠EAD、∠DAC、∠C的度数. 如图,用数字标注的角中,共有四对内错角,请把它们一一写出,并说明哪两条直线被哪一条直线所截得的内错角.
如图,用数字标注的角中,共有四对内错角,请把它们一一写出,并说明哪两条直线被哪一条直线所截得的内错角. 如图,AB∥CD,直线EF分别交AB、CD分于点E、F,FH平分∠EFD,若∠1=110°,则∠2=
如图,AB∥CD,直线EF分别交AB、CD分于点E、F,FH平分∠EFD,若∠1=110°,则∠2= 如图,已知:AB=CB,AD=CD,求证:∠A=∠C.
如图,已知:AB=CB,AD=CD,求证:∠A=∠C. 如图,已知?ABCD的周长为30cm,AE⊥BC于点E,AF⊥DC于点F,AE:AF=2:3,∠C=120°,求?ABCD的面积.
如图,已知?ABCD的周长为30cm,AE⊥BC于点E,AF⊥DC于点F,AE:AF=2:3,∠C=120°,求?ABCD的面积.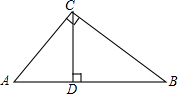 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h.求证: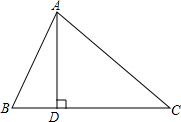 如图所示,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°,AB=2cm.
如图所示,在△ABC中,AD⊥BC,垂足为点D,∠B=60°,∠C=45°,AB=2cm.