题目内容
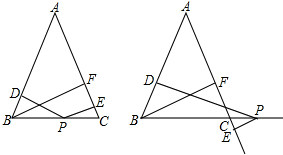
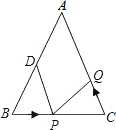 如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.(1)若点Q的运动速度与P点相同,经过3s后,△BPD与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与P点不相同,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(3)若点Q以(2)中的速度从C点出发,P点以原来的速度从B点同时出发,都沿△ABC三边逆时针运动,求经过多长时间,P点与Q点第一次在△ABC的什么位置上相遇?
考点:全等三角形的判定
专题:动点型
分析:(1)根据题意BP=3,CQ=3,求出BD=CP=5,再由∠B=∠C,即可证明△BPD≌△CQP;
(2)分类讨论:①当BP=CP时,②当BP=CQ时,分别求出t的值即可得出结果;
(3)两点相遇时,路程差为10+10,即可求出时间t的值.
(2)分类讨论:①当BP=CP时,②当BP=CQ时,分别求出t的值即可得出结果;
(3)两点相遇时,路程差为10+10,即可求出时间t的值.
解答:解:(1)经过3秒后,△BPD≌△CQP;此时BP=3,CQ=3,
∵D是AB的中点,AB=AC=10,BC=8,
∴BD=5,CP=8-3=5,∠B=∠C,
∴BP=CQ,BD=CP,
在△BPD和△CQP中,
∴△BPD≌△CQP(SAS);
(2)∵∠B=∠C,
∴PD与PQ是对应边,
若△BPD≌△CQP,设点Q的速度为xcm/s,时间为t秒;
分两种情况:①当BP=CP时,CQ=BD=5,
∵BC=8,
∴BP=4,t=4,
∴x=5÷4=
;
②当BP=CQ时,xt=t,x=1,不合题意;
综上所述:Q的运动速度为
cm/s时,△BPD≌△CQP;
(3)设经过t秒时,两点第一次相遇;根据题意得:
t-t=10+10,
解得:t=80,
∵80÷(10+10+8)=3…16,
即经过100秒,P点与Q点第一次在AB边上距离B点4cm处相遇.
∵D是AB的中点,AB=AC=10,BC=8,
∴BD=5,CP=8-3=5,∠B=∠C,
∴BP=CQ,BD=CP,
在△BPD和△CQP中,
|
∴△BPD≌△CQP(SAS);
(2)∵∠B=∠C,
∴PD与PQ是对应边,
若△BPD≌△CQP,设点Q的速度为xcm/s,时间为t秒;
分两种情况:①当BP=CP时,CQ=BD=5,
∵BC=8,
∴BP=4,t=4,
∴x=5÷4=
| 5 |
| 4 |
②当BP=CQ时,xt=t,x=1,不合题意;
综上所述:Q的运动速度为
| 5 |
| 4 |
(3)设经过t秒时,两点第一次相遇;根据题意得:
| 5 |
| 4 |
解得:t=80,
∵80÷(10+10+8)=3…16,
即经过100秒,P点与Q点第一次在AB边上距离B点4cm处相遇.
点评:本题考查了全等三角形的判定方法;特别是利用分类讨论的方法讨论三角形全等的情况,培养学生综合解题的能力.

练习册系列答案
相关题目
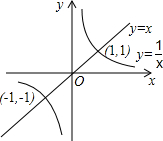 我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>
我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙.比如,通过图中的信息我们可以得出x>| 1 |
| x |
| A、x>1 |
| B、-1<x<0 |
| C、x>1或-1<x<0 |
| D、以上都不对 |
 如图,在Rt△ABC中,∠C=90°,投影线方向如图所示,点C在斜边AB上的正投影为点D,
如图,在Rt△ABC中,∠C=90°,投影线方向如图所示,点C在斜边AB上的正投影为点D, 如图,线段AB上有一点C,且AC=2BC,D是AB中点,已知CD长为2cm,求BC、AB的长.
如图,线段AB上有一点C,且AC=2BC,D是AB中点,已知CD长为2cm,求BC、AB的长.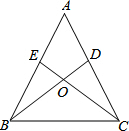 已知:如图,在△ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ABD=∠ACE.BD与CE相交于点O.求证:(1)OB=OC;(2)BE=CD.
已知:如图,在△ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ABD=∠ACE.BD与CE相交于点O.求证:(1)OB=OC;(2)BE=CD.
 求图中的三视图所表示的几何体的体积.
求图中的三视图所表示的几何体的体积. 如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.