题目内容
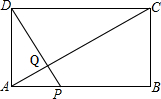 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.
①当t为何值时,DP⊥AC?
②设S△APQ+S△DCQ=y,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
考点:相似形综合题
专题:压轴题,探究型
分析:(1)求证相似,证两对角相等即可,由平行线的性质容易得出角相等.
(2)①当垂直时,易得三角形相似,故有相似边成比例,由题中已知矩形边长,AP长已知,故t易知.
②因为S△APQ+S△DCQ=y,故求S△APQ和S△DCQ是解决问题的关键,观察无固定组合规则图象,则考虑作高分别求取.考虑两高在同一直线上,且相加恰为10,故可由(1)相似结论得,高的比等于对应边长比,设其中一高为h,即可求得,则易表示y=
,注意要考虑t的取值.讨论何时y最小,y=
不是我们学过的函数类型,故无法用最值性质来讨论,观察题目问法“探究P点运动到第几秒到第几秒之间时”,<1>并不是我们常规的在确定时间最小,<2>时间为整数秒.故可考虑将所有可能的秒全部算出,再观察数据探究函数的变化找结论.
(2)①当垂直时,易得三角形相似,故有相似边成比例,由题中已知矩形边长,AP长已知,故t易知.
②因为S△APQ+S△DCQ=y,故求S△APQ和S△DCQ是解决问题的关键,观察无固定组合规则图象,则考虑作高分别求取.考虑两高在同一直线上,且相加恰为10,故可由(1)相似结论得,高的比等于对应边长比,设其中一高为h,即可求得,则易表示y=
| 5t2+2000 |
| 20+t |
| 5t2+2000 |
| 20+t |
解答:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠QPA=∠QDC,∠QAP=∠QCD,
∴△APQ∽△CDQ.
(2)解:①当DP⊥AC时,∠QCD+∠QDC=90°,
∵∠ADQ+∠QDC=90°,
∴∠DCA=∠ADP,
∵∠ADC=∠DAP=90°,
∴△ADC∽△PAD,
∴
=
,
∴
=
,
解得 PA=5,
∴t=5.
②设△AQP的边AP上的高h,则△QDC的边DC上的高为(10-h).
∵△APQ∽△CDQ,
∴
=
=
,
解得 h=
,
∴10-h=
,
∴S△APQ=
•AP•h=
,
S△DCQ=
•DC•(10-h)=
,
∴y=S△APQ+S△DCQ=
+
=
(0≤t≤20).
探究:
t=0,y=100;
t=1,y≈95.48;
t=2,y≈91.82;
t=3,y≈88.91;
t=4,y≈86.67;
t=5,y=85;
t=6,y≈83.85;
t=7,y≈83.15;
t=8,y≈82.86;
t=9,y≈82.93;
t=10,y≈83.33;
t=11,y≈84.03;
t=12,y=85;
t=13,y≈86.21;
t=14,y≈87.65;
t=15,y≈89.29;
t=16,y≈91.11;
t=17,y≈93.11;
t=18,y≈95.26;
t=19,y≈97.56;
t=20,y=100;
观察数据知:
当0≤t≤8时,y随t的增大而减小;
当9≤t≤20时,y随t的增大而增大;
故y在第8秒到第9秒之间取得最小值.
∴AB∥CD,
∴∠QPA=∠QDC,∠QAP=∠QCD,
∴△APQ∽△CDQ.
(2)解:①当DP⊥AC时,∠QCD+∠QDC=90°,
∵∠ADQ+∠QDC=90°,
∴∠DCA=∠ADP,
∵∠ADC=∠DAP=90°,
∴△ADC∽△PAD,
∴
| AD |
| PA |
| DC |
| AD |
∴
| 10 |
| PA |
| 20 |
| 10 |
解得 PA=5,
∴t=5.
②设△AQP的边AP上的高h,则△QDC的边DC上的高为(10-h).
∵△APQ∽△CDQ,
∴
| h |
| 10-h |
| AP |
| DC |
| t |
| 20 |
解得 h=
| 10t |
| 20+t |
∴10-h=
| 200 |
| 20+t |
∴S△APQ=
| 1 |
| 2 |
| 5t2 |
| 20+t |
S△DCQ=
| 1 |
| 2 |
| 2000 |
| 20+t |
∴y=S△APQ+S△DCQ=
| 5t2 |
| 20+t |
| 2000 |
| 20+t |
| 5t2+2000 |
| 20+t |
探究:
t=0,y=100;
t=1,y≈95.48;
t=2,y≈91.82;
t=3,y≈88.91;
t=4,y≈86.67;
t=5,y=85;
t=6,y≈83.85;
t=7,y≈83.15;
t=8,y≈82.86;
t=9,y≈82.93;
t=10,y≈83.33;
t=11,y≈84.03;
t=12,y=85;
t=13,y≈86.21;
t=14,y≈87.65;
t=15,y≈89.29;
t=16,y≈91.11;
t=17,y≈93.11;
t=18,y≈95.26;
t=19,y≈97.56;
t=20,y=100;
观察数据知:
当0≤t≤8时,y随t的增大而减小;
当9≤t≤20时,y随t的增大而增大;
故y在第8秒到第9秒之间取得最小值.
点评:本题主要考查了三角形相似及相似图形性质等问题,(2)②是一道非常新颖的考点,它考察了考生对函数本身的理解,作为未知函数类型如何探索其变化趋势是非常需要学生能力的.总体来说,本题是一道非常好、非常新的题目.

练习册系列答案
相关题目
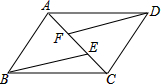 如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.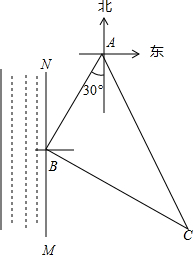 如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水,然后沿另一方向走80m到达菜地C处浇水,最后沿第三方向走100m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水,然后沿另一方向走80m到达菜地C处浇水,最后沿第三方向走100m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由. 如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.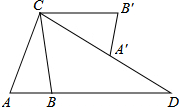 如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为
如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 如图,按此规律,第6行最后一个数字是
如图,按此规律,第6行最后一个数字是