题目内容
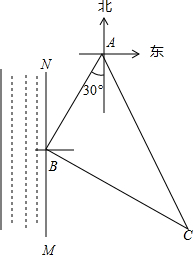 如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水,然后沿另一方向走80m到达菜地C处浇水,最后沿第三方向走100m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.
如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水,然后沿另一方向走80m到达菜地C处浇水,最后沿第三方向走100m回到家A处.问小明在河边B处取水后是沿哪个方向行走的?并说明理由.考点:勾股定理的逆定理,方向角
专题:应用题
分析:首先根据勾股定理逆定理得出∠ABC=90°,然后再判断AD∥NM,可得∠NBA=∠BAD=30°,再根据平角定义可得∠MBC=180°-90°-30°=60°,进而得到答案.
解答: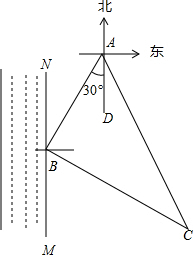 解:∵AB=60,BC=80,AC=100,
解:∵AB=60,BC=80,AC=100,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴AD∥NM,
∴∠NBA=∠BAD=30°,
∴∠MBC=180°-90°-30°=60°,
∴小明在河边B处取水后是沿南偏东60°方向行走的.
 解:∵AB=60,BC=80,AC=100,
解:∵AB=60,BC=80,AC=100,∴AB2+BC2=AC2,
∴∠ABC=90°,
∴AD∥NM,
∴∠NBA=∠BAD=30°,
∴∠MBC=180°-90°-30°=60°,
∴小明在河边B处取水后是沿南偏东60°方向行走的.
点评:此题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
 △ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,
△ABC为等边三角形,边长为a,DF⊥AB,EF⊥AC,
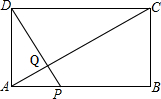 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q. 如图,将四个圆两两相切拼接在一起,它们的半径均为1cm,则中间阴影部分的面积为
如图,将四个圆两两相切拼接在一起,它们的半径均为1cm,则中间阴影部分的面积为 在△ABC中,点M是AB边的中点,点E是BC上一点,AC的延长线与ME的延长线交于点F,若CE:EB=1:3,则AC:AF=
在△ABC中,点M是AB边的中点,点E是BC上一点,AC的延长线与ME的延长线交于点F,若CE:EB=1:3,则AC:AF=