题目内容
一个三角形纸板,三边长分别为10cm,10cm,12cm,在这个纸板上剪出一个面积最大的正方形,则此正方形的边长为 cm.
考点:相似三角形的应用,二次函数的最值
专题:
分析:根据题意画出图形,先根据等腰三角形的性质求出BD的长,再根据勾股定理求出AD的长,设正方形的边长为x,由△BEG∽△BDA即可得出结论.
解答: 解:如图所示,△ABC中AB=10cm,AC=10cm,BC=12cm,
解:如图所示,△ABC中AB=10cm,AC=10cm,BC=12cm,
AD为△ABC的高,
∵AD⊥BC,
∴BD=
BC=6cm,
∴AD=
=
=8cm,
设正方形的边长为x,则GE=xcm,DE=
xcm,
BE=6-
xcm,
∵GE⊥BC,AD⊥BC,
∴△BEG∽△BDA,
∴
=
,
=
,解得x=4.8cm.
故答案为:4.8cm.
 解:如图所示,△ABC中AB=10cm,AC=10cm,BC=12cm,
解:如图所示,△ABC中AB=10cm,AC=10cm,BC=12cm,AD为△ABC的高,
∵AD⊥BC,
∴BD=
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
| 102-62 |
设正方形的边长为x,则GE=xcm,DE=
| 1 |
| 2 |
BE=6-
| 1 |
| 2 |
∵GE⊥BC,AD⊥BC,
∴△BEG∽△BDA,
∴
| GE |
| AD |
| BE |
| BD |
| x |
| 8 |
6-
| ||
| 6 |
故答案为:4.8cm.
点评:本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若α,β是方程x2-2x-3=0的两个实数根,则α2+β2的值为( )
| A、10 | B、9 | C、7 | D、5 |
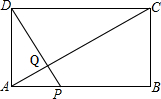 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q. 如图,将四个圆两两相切拼接在一起,它们的半径均为1cm,则中间阴影部分的面积为
如图,将四个圆两两相切拼接在一起,它们的半径均为1cm,则中间阴影部分的面积为 在△ABC中,点M是AB边的中点,点E是BC上一点,AC的延长线与ME的延长线交于点F,若CE:EB=1:3,则AC:AF=
在△ABC中,点M是AB边的中点,点E是BC上一点,AC的延长线与ME的延长线交于点F,若CE:EB=1:3,则AC:AF=