题目内容
1.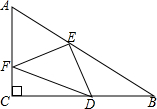 如图,在△ABC中,∠C=90°,∠B=30°,CB=4,点D是CB的中点,点E,F分别在AB,AC上,则△DEF的周长的最小值是2$\sqrt{7}$.
如图,在△ABC中,∠C=90°,∠B=30°,CB=4,点D是CB的中点,点E,F分别在AB,AC上,则△DEF的周长的最小值是2$\sqrt{7}$.
分析 作D关于AC的对称点G,作D关于AB的对称点H,连接GH交AC于FAB于E,则GH=△DEF的周长的最小值,由点D是CB的中点,得到BD=CD=2,根据已知条件得到DH=2DQ=4,∠HDB=60°,过H作HP⊥BC于P,解直角三角形得到PD=$\frac{1}{2}$DH=1,PH=$\sqrt{3}$,根据勾股定理即可得到结论.
解答 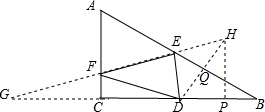 解:作D关于AC的对称点G,作D关于AB的对称点H,连接GH交AC于FAB于E,
解:作D关于AC的对称点G,作D关于AB的对称点H,连接GH交AC于FAB于E,
则GH=△DEF的周长的最小值,
∵点D是CB的中点,
∴BD=CD=2,
∵∠B=30°,
∴DH=2DQ=4,∠HDB=60°
过H作HP⊥BC于P,
∴PD=$\frac{1}{2}$DH=1,PH=$\sqrt{3}$,
∵DG=2CD=4,
∴PG=5,
∴HG=$\sqrt{P{H}^{2}+P{G}^{2}}$=2$\sqrt{7}$.
∴△DEF的周长的最小值是2$\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 本题考查的是最短线路问题及直角三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若式子$\frac{\sqrt{x-1}}{x+2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥1且x≠0 | B. | x>1 且x≠-2 | C. | x≥1 | D. | x≥1 且x≠-2 |
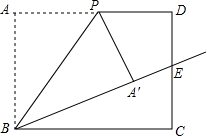 如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.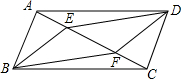 如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.
如图,E、F是?ABCD对角线AC上的两点,且BE∥DF,求证:BF=DE.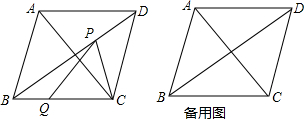 如图,菱形ABCD中,∠ABC<90°,P为该菱形对角线BD上一动点,Q为BC边上一动点,若AC=30,PC+PQ的最小值为24,求菱形ABCD的边长(要求在备用图中画出必要的图形)
如图,菱形ABCD中,∠ABC<90°,P为该菱形对角线BD上一动点,Q为BC边上一动点,若AC=30,PC+PQ的最小值为24,求菱形ABCD的边长(要求在备用图中画出必要的图形)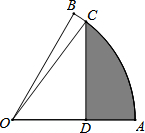 如图,扇形OAB中,∠AOB=60°,扇形半径为3,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为$\frac{9}{8}π-\frac{9}{4}$.
如图,扇形OAB中,∠AOB=60°,扇形半径为3,点C在AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为$\frac{9}{8}π-\frac{9}{4}$.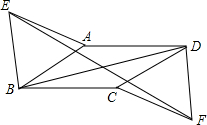 如图,在?ABCD中,分别以AB、CD为边向外作等边△ABE和等边△CDF,
如图,在?ABCD中,分别以AB、CD为边向外作等边△ABE和等边△CDF,