题目内容
1.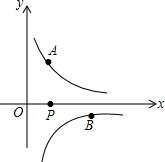 如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).
如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).
分析 先求出A、B两点的坐标,作点A关于x轴的对称点A′,连接A′B交x轴于点P呢点P即为所求点.
解答 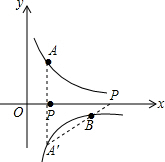 解:∵点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上,
解:∵点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上,
∴A($\frac{1}{2}$,2),B(2,-$\frac{1}{2}$).
作点A关于x轴的对称点A′,则A′($\frac{1}{2}$,-2),
∵|PA-PB|≤A′B,
∴直线AB与x轴的交点即为点P.
设直线A′B的解析式为y=kx+b(k≠0),
∵A′($\frac{1}{2}$,-2),B(2,-$\frac{1}{2}$),
∴$\left\{\begin{array}{l}-2=\frac{1}{2}k+b\\-\frac{1}{2}=2k+b\end{array}\right.$,解得$\left\{\begin{array}{l}k=1\\ b=-\frac{5}{2}\end{array}\right.$,
∴直线A′B的解析式为y=x-$\frac{5}{2}$,
∴P($\frac{5}{2}$,0).
故答案为:($\frac{5}{2}$,0).
点评 本题考查的是反比例函数图象上点的坐标特点,先根据题意得出A、B两点的坐标是解答此题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
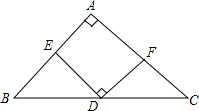 如下图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,ED⊥FD且分别交AB、AC于E、F.求证:BE=AF.
如下图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,ED⊥FD且分别交AB、AC于E、F.求证:BE=AF.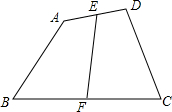 四边形ABCD中,E,F分别为AD,BC的中点,EF=m,则AB+CD的最小值为2m.
四边形ABCD中,E,F分别为AD,BC的中点,EF=m,则AB+CD的最小值为2m. 如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.
如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.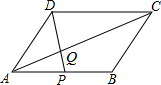 如图,在?ABCD中,点P在AB上,连结DP,交AC于点Q,当点P是AB的中点时,△ADQ的面积为1,则?ABCD的面积为( )
如图,在?ABCD中,点P在AB上,连结DP,交AC于点Q,当点P是AB的中点时,△ADQ的面积为1,则?ABCD的面积为( )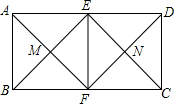 如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( )个正方形.
如图所示,在矩形ABCD中,AD=2AB,E,F分别是AD,BC的中点,连结AF与BE,CE与DF分别交于点M,N,连结EF,则图中一共有( )个正方形.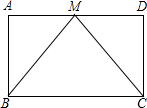 已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.
已知:如图,在?ABCD中,M是AD的中点,连接BM、CM,且BM=CM,求证:?ABCD是矩形.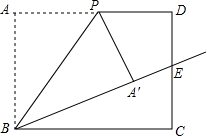 如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.
如图,在矩形ABCD中,AB=10,BC=12,P是边AD上的一个动点,将△ABP沿着BP折叠,得到△′ABP.若射线BA′恰好经过边CD的中点E,则四边形DPA′E的面积为$\frac{70}{3}$.