题目内容
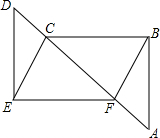 如图,点A、F、C、D在同一条直线上,且AB=DE,BC=EF,AF=CD.
如图,点A、F、C、D在同一条直线上,且AB=DE,BC=EF,AF=CD.求证:①BC∥EF;
②BF=CE.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)要证明BC∥EF,先证明△ABC≌△DEF,得到对应角相等,然后利用内错角相等即可证明两直线平行;
(2)根据(1)得,∠BCF=EFC,再证明△BCF≌△EFC,即可得出BF=CE.
(2)根据(1)得,∠BCF=EFC,再证明△BCF≌△EFC,即可得出BF=CE.
解答:证明:(1)∵AF=CD,
∴AF+FC=CD+FC即AC=DF.
∵AB∥DE,
∴∠A=∠D.
∵AB=DE,
在△ABC和△DEF中,
.
∴△ABC≌△DEF(SAS).
∴∠ACB=∠DFE.
∴EF∥BC.
(2)∵△ABC≌△DEF(已证),
∴∠ACB=∠DFE.
在△BCF和△EFC中,
.
∴△BCF≌△EFC(SAS).
∴BF=CE.
∴AF+FC=CD+FC即AC=DF.
∵AB∥DE,
∴∠A=∠D.
∵AB=DE,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS).
∴∠ACB=∠DFE.
∴EF∥BC.
(2)∵△ABC≌△DEF(已证),
∴∠ACB=∠DFE.
在△BCF和△EFC中,
|
∴△BCF≌△EFC(SAS).
∴BF=CE.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
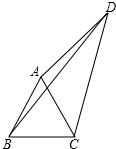 如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为
如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为 如图,已知AB=CD,AE=DF,CE=BF.
如图,已知AB=CD,AE=DF,CE=BF. 某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图所示,那么运动员公寓应建立在何处?
某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图所示,那么运动员公寓应建立在何处?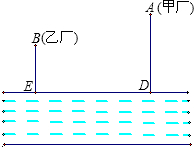 如图,大江的一侧有甲、乙两家工厂,它们都有垂直于江边的小路,长度分别为m千米和n千米,两条小路相距l千米.现在要在江边建一个抽水站,把水送到甲、乙两厂去.欲使供水管路最短,抽水站应建在哪里?
如图,大江的一侧有甲、乙两家工厂,它们都有垂直于江边的小路,长度分别为m千米和n千米,两条小路相距l千米.现在要在江边建一个抽水站,把水送到甲、乙两厂去.欲使供水管路最短,抽水站应建在哪里?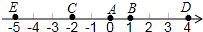 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动 如图,在△ABC中,∠B=∠C,AD是BC边上的中线,E是AC上一点且DE=AE,求证:DE∥AB.
如图,在△ABC中,∠B=∠C,AD是BC边上的中线,E是AC上一点且DE=AE,求证:DE∥AB.