题目内容
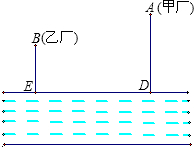如图，大江的一侧有甲、乙两家工厂，它们都有垂直于江边的小路，长度分别为m千米和n千米，两条小路相距l千米．现在要在江边建一个抽水站，把水送到甲、乙两厂去．欲使供水管路最短，抽水站应建在哪里？考点：轴对称-最短路线问题,作图—应用与设计作图
专题：
分析：作出点B关于河岸的对称点B′，连接AB′，根据轴对称确定最短路线问题，AB′与河岸的交点即为所求的建立抽水站的地方，然后根据相似三角形对应边成比例列式求出EP的长度，即可得解．
解答：
解：如图，抽水站建立在点P处，
∵BE⊥直线l，
∴B′E⊥直线l，
又∵AD⊥直线l，
∴△B′EP∽△ADP，
∴
=
，
即
=
，
解得EP=
，
即抽水站建立在距离E点
米处．
解：如图，抽水站建立在点P处，∵BE⊥直线l，
∴B′E⊥直线l，
又∵AD⊥直线l，
∴△B′EP∽△ADP，
∴
| B′E |
| EP |
| AD |
| PD |
即
| m |
| EP |
| n |
| l-EP |
解得EP=
| ml |
| m+n |
即抽水站建立在距离E点
| ml |
| m+n |
点评：本题考查了轴对称确定最短路线问题，相似三角形的判定与性质，熟记最短路径的确定方法是解题的关键，本题需求出抽水站到点E的距离．
练习册系列答案
相关题目
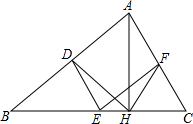如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．
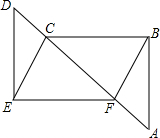如图，点A、F、C、D在同一条直线上，且AB=DE，BC=EF，AF=CD．
如图，AD是△ABC的角平分线，过点D分别作AC和AB的平行线，交AB于点E，交AC于点F．求证：四边形AEDF是菱形．
在△ABC中，AB=AC，点E，F分别在AB，AC上，∠AEC=∠AFB，BF与CE相交于点P