题目内容
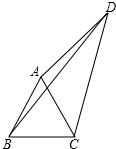 如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为
如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为考点:全等三角形的判定与性质,勾股定理
专题:计算题
分析:如图,以CD为边作等边△CDE,连接AE,根据三角形ABC与三角形CDE为等边三角形,利用等边三角形的性质得到两对边相等,利用等式的性质得到夹角相等,利用SAS得到三角形BCD与三角形ACE全等,利用全等三角形对应边相等得到BD=AE,求出AE的长,由∠ADC+∠CDE=∠ADE=90°,得到三角形ADE为直角三角形,利用勾股定理求出DE的长,即为DC的长,在三角形ADC中,利用三角形的面积公式即可求出三角形ADC面积.
解答: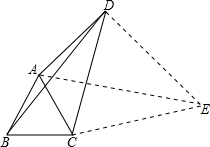 解:如图,以CD为边作等边△CDE,连接AE,
解:如图,以CD为边作等边△CDE,连接AE,
∵△ABC与△CDE为等边三角形,
∴∠BCD=∠BCA+∠ACD=∠DCE+∠ACD=∠ACE,
在△BCD和△ACE中,
,
∴△BCD≌△ACE(SAS),
∴BD=AE,
∵∠ADC=30°,
∴∠ADE=90°,
在Rt△ADE中,AE=5,AD=3,
根据勾股定理得:DE=
=4,
∴CD=DE=4,
则S=
AD•DC•sin30°=
×3×4×
=3.
故答案为:3.
 解:如图,以CD为边作等边△CDE,连接AE,
解:如图,以CD为边作等边△CDE,连接AE,∵△ABC与△CDE为等边三角形,
∴∠BCD=∠BCA+∠ACD=∠DCE+∠ACD=∠ACE,
在△BCD和△ACE中,
|
∴△BCD≌△ACE(SAS),
∴BD=AE,
∵∠ADC=30°,
∴∠ADE=90°,
在Rt△ADE中,AE=5,AD=3,
根据勾股定理得:DE=
| AE2-AD2 |
∴CD=DE=4,
则S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:3.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
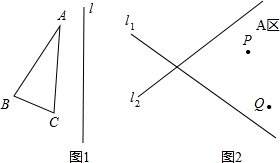 (1)画出图1中△ABC关于直线L的对称图形△A′B′C′.
(1)画出图1中△ABC关于直线L的对称图形△A′B′C′.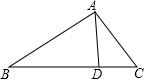 如图,点D是△ABC的边BC上一点,已知AC=3,CD=
如图,点D是△ABC的边BC上一点,已知AC=3,CD=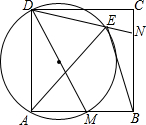 如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.
如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.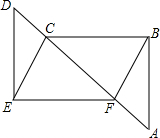 如图,点A、F、C、D在同一条直线上,且AB=DE,BC=EF,AF=CD.
如图,点A、F、C、D在同一条直线上,且AB=DE,BC=EF,AF=CD.