��Ŀ����
7����ͼ��������ABCD�У���BAD=��B=��C=��D=90�㣬AB=CD=4��AD=BC����M�DZ�BC�ϵ�һ����BM=3����P�DZ�AD��DC��һ�㣮��1����ͼ1�����ABM���ܳ����ı���AMCD���ܳ�=1��2�����AD�ij���
��2����ͼ2������P���D�غ��ҡ�AMP=90�㣬��AP�ij���
��3������ͼ3�����AD=4����AMPΪ���������Σ����AMP�������
��ֱ��д��ʹ��AMPΪ����������ʱ��P����м�����

���� ��1����CM=x����x�ֱ��ʾ����ABM���ܳ����ı���AMCD���ܳ������������г����̣��ⷽ�̼��ɣ�
��2�����ݹ��ɶ����г����̣��ⷽ�����AP��
��3���ٷ�AM=AP��PA=PM������������ݵ��������ε����ʺ��ɶ������
�ڽ��ͼ�Ρ����ݵ��������ε����ʽ��
��� �⣺��1����CM=x��
�ߡ�B=90�㣬AB=4��BM=3��
�ɹ��ɶ�����AM=5��
���ABM���ܳ�=AB+BM+AM=12���ı���AMCD���ܳ�=x+3+4+5+x=2x+12��
������ã�12����2x+12��=1��2��
��ã�x=6����CM=6��
��AD=9��
��2����CM=x��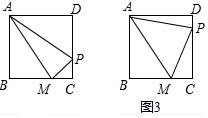
��Rt��CMP��DM2=CM2+CD2=x2+42
��RT��AMP��DM2=AD2-AM2=��x+3��2-52
��x2+42=��x+3��2-52
��ã�x=$\frac{16}{3}$��
��AP=$3+\frac{16}{3}=\frac{25}{3}$��
��3������ͼ3����AM=APʱ��
AP=5��AD=4��
�ɹ��ɶ����ã�DP=3��
��MC=PC=1��
��AMP�����=4��4-$\frac{1}{2}$��3��4-$\frac{1}{2}$��3��4-$\frac{1}{2}$��1��1=3.5��
��PA=PMʱ��
��DP=y����CP=4-y��
��42+y2=12+��4-y��2��
��ã�y=$\frac{1}{8}$����DP=$\frac{1}{8}$��
��AMP�����=4��4-$\frac{1}{2}$��3��4-$\frac{1}{2}$��$\frac{1}{8}$��4-$\frac{1}{2}$��1��$\frac{31}{8}$=$\frac{125}{16}$��
������������AMP �����Ϊ3.5��$\frac{125}{16}$��
�ڵ���P���߶�AD��ʱ��AM=AP��MA=MP��
����P���߶�CD��ʱ��AM=AP��PA=MP��
��P�����4����
���� ���⿼����Ǿ��ε����ʡ����ɶ�����Ӧ�ã����վ��ε����ʡ������ε������ʽ��������ù��ɶ����ǽ���Ĺؼ���

| A�� | 1 | B�� | -1 | C�� | -7 | D�� | 7 |
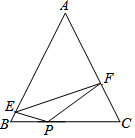 ��֪����ͼ���ڡ�ABC�У�AB=AC��tanA=$\frac{4}{3}$��PΪBC��һ�㣬��BP��PC=3��5��E��F�ֱ�ΪAB��AC�ϵĵ㣬�ҡ�EPF=2��B������EPF�����Ϊ6����EF=2$\sqrt{13}$��
��֪����ͼ���ڡ�ABC�У�AB=AC��tanA=$\frac{4}{3}$��PΪBC��һ�㣬��BP��PC=3��5��E��F�ֱ�ΪAB��AC�ϵĵ㣬�ҡ�EPF=2��B������EPF�����Ϊ6����EF=2$\sqrt{13}$��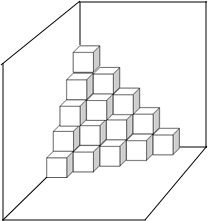 ��ͼ���ǰ����ɰڷ���ǽ�ǵ�һЩС�����壬�������·ֱ��Ϊ��һ�㣬�ڶ��㣬�����㡭��n�㡭
��ͼ���ǰ����ɰڷ���ǽ�ǵ�һЩС�����壬�������·ֱ��Ϊ��һ�㣬�ڶ��㣬�����㡭��n�㡭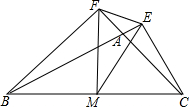 ��ͼ���ڡ�ABC�У�CE��BA���ӳ�����E��BF��CA���ӳ�����F��MΪBC���е㣬�ֱ�����ME��MF��EF��
��ͼ���ڡ�ABC�У�CE��BA���ӳ�����E��BF��CA���ӳ�����F��MΪBC���е㣬�ֱ�����ME��MF��EF��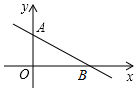 ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{1}{2}$x+2��x��y�ύ��A��B���㣬�ڵڶ���������һ��P��ʹ��PAO�͡�AOB���Ƶ������θ���Ϊ��������
ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{1}{2}$x+2��x��y�ύ��A��B���㣬�ڵڶ���������һ��P��ʹ��PAO�͡�AOB���Ƶ������θ���Ϊ��������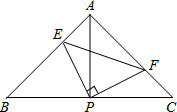 ��ͼ����֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�����������ĸ����ۣ�
��ͼ����֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�����������ĸ����ۣ�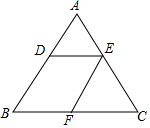 ��֪����ͼ����ABC�У�DE��BC��
��֪����ͼ����ABC�У�DE��BC��