题目内容
15.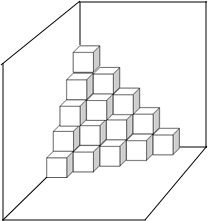 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…(1)第三层有6个小正方体.
(2)从第四层至第六层(含第四层和第六层)共有46个小正方体.
(3)第n层有$\frac{n(n+1)}{2}$个小正方体.
(4)若每个小正方体边长为a分米,共摆放了n层,则要将摆放的小正方体能看到的表面部分涂上防锈漆,则防锈漆的总面积为$\frac{3}{2}$a2n(n+1)分米2.
分析 (1)第1个图有1层,共1个小正方体,第2个图有2层,第2层正方体的个数为1+2,以此类推第三层即可;
(2)第4至6层求出每层个数相加即可;
(3)根据相应规律可得第n层正方体的个数为1+2+3+…+n=$\frac{n(n+1)}{2}$;
(4)共摆放n层,根据靠墙小正方形的面的个数和与地面接触小正方形的面的个数,求出总面数再乘每一个小正方形的面积即可.
解答 解:(1)第1层,共1个小正方体,
第2层正方体的个数为1+2=3,
第3层正方体的个数为:1+2+3=6.
故答案为:6.
(2)第4层正方体的个数为:10,
第5层正方体的个数为:15,
第6层正方体的个数为:21,
所以从第四层至第六层(含第四层和第六层)共有:10+15+21=46.
故答案为:46.
(3)根据(1)相应规律,可得第n层正方体的个数为1+2+3+…+n=$\frac{n(n+1)}{2}$;
(4)共摆放n层,则靠墙小正方形的面的个数:2×(1+2+3+…+n)=n(n+1),
地面接触小正方形的面的个数:1+2+3+…+n=$\frac{n(n+1)}{2}$,
所以靠墙及地面的部分涂上防锈漆的面积为:[n(n+1)+$\frac{n(n+1)}{2}$]×a2=$\frac{3}{2}$a2n(n+1)分米2.
故答案为:(1)6;(2)41;(3)$\frac{n(n+1)}{2}$;(4)$\frac{3}{2}$a2n(n+1).
点评 此题考查图形规律性的变化,得到第n层正方体的个数的规律是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知A、B在数轴上分别表示a、b.
(1)对照数轴填写下表:
(2)若A、B两点间的距离记为d,试问d和a、b(a<b)有何数量关系;
(3)写出数轴上到-1和1的距离之和为2的所有整数;
(4)若点C表示的数为x,代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2,此时代数式|x+1|+|x-2|的最小值是3.
(1)对照数轴填写下表:
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
(3)写出数轴上到-1和1的距离之和为2的所有整数;
(4)若点C表示的数为x,代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2,此时代数式|x+1|+|x-2|的最小值是3.
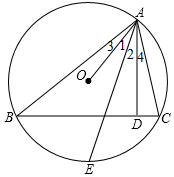 △ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).
△ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).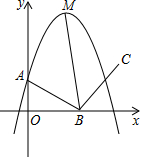 如图,抛物线y=-2x2+4x+1交y轴点A,顶点是M,点B是x轴上的一个动点,连结AB,BM,将线段AB绕点B顺时针旋转90°到BC的位置,当BM平分∠ABC时,点B的坐标是(1,0)或(2,0).
如图,抛物线y=-2x2+4x+1交y轴点A,顶点是M,点B是x轴上的一个动点,连结AB,BM,将线段AB绕点B顺时针旋转90°到BC的位置,当BM平分∠ABC时,点B的坐标是(1,0)或(2,0).