Question

2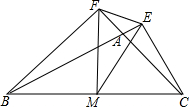．如图，在△ABC中，CE⊥BA的延长线于E，BF⊥CA的延长线于F，M为BC的中点，分别连接ME、MF、EF．
（1）若EF=3，BC=10，求△EFM的周长；
（2）若∠ABC=29°，∠ACB=46°，求∠EMF的度数．

Answer 1

分析 （1）根据直角三角形斜边中线的性质得出EM=FM=$\frac{1}{2}$BC=5，进而可求得△EFM的周长；
（2）根据直角三角形斜边中线的性质得出EM=BM，FM=MC，根据等腰三角形的性质和三角形内角和定理得出∠EMC=58°，∠FMC=88°，进而可求得∠FME=88°-58°=30°．

解答 解：（1）∵CE⊥BA，M为BC的中点，
∴EM=$\frac{1}{2}$BC=4，
∵BF⊥CA，M为BC的中点，
∴FM=$\frac{1}{2}$BC=4，
∴△EFM的周长为：EM+FM+EF=5+5+3=13；

（2）∵EM=$\frac{1}{2}$BC，M为BC的中点，
∴BM=EM，
∴∠EBM=∠BEM=29°，
∴∠EMC=58°，
∵FM=$\frac{1}{2}$BC，M为BC的中点，
∴FM=MC，
∴∠MFC=∠ACB=46°，
∴∠FMC=88°，
∴∠FME=88°-58°=30°．

点评 本题考查了直角三角形斜边中线的性质，等腰三角形的性质，三角形外角的性质以及三角形内角和定理，熟练掌握性质定理是解题的关键．