Question

19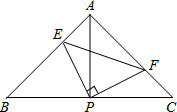．如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出以下四个结论：
①AE=CF；  
②△EPF是等腰直角三角形；
③S_{四边形AEPF}=$\frac{1}{2}$S_△ABC；  
④BE+CF=EF．
⑤当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合）．
上述结论中始终正确的有①②③（填序号）．

Answer 1

分析 根据图形旋转的性质及全等三角形的判定定理得出△APE≌△CPF，再根据全等三角形的性质对题中的结论逐一判断，即可得出结论．

解答 解：∵∠APE、∠CPF都是∠APF的余角，
∴∠APE=∠CPF，
∵AB=AC，∠BAC=90°，P是BC中点，
∴AP=CP，
在△APE与△CPF中，$\left\{\begin{array}{l}{∠APE=∠CPF}&{\;}\\{AP=CP}&{\;}\\{∠EPA=∠FPC}&{\;}\end{array}\right.$，
∴△APE≌△CPF（ASA），
∴AE=CF，∴S_△APE=S_△CPF，
∵∠EPF=90°，
∴△EPF是等腰直角三角形，
S_{四边形AEPF}=S_△APC=$\frac{1}{2}$S_△ABC，①②③正确；
∵BE+CF=BE+AE=AB，只有当E与A、B重合时，BE+CF=EF．
∴④不正确；
故答案为：①②③．

点评 本题考查的是等腰直角三角形的性质及全等三角形的判定与性质，图形旋转的性质，根据题意得出△APE≌△CPF是解答此题的关键．