题目内容
14．
如图，一次函数与反比例函数y=$\frac{k}{x}$的图象交于点A（-6，-3）和B（a，6）（1）求反比例函数的表达式和点B的坐标；
（2）根据图象写出使一次函数值大于反比例函数值x的取值范围．
分析 （1）根据反比例函数y=$\frac{k}{x}$的图象过点（-6，-3）和B（a，6），利用待定系数法求出即可；
（2）根据（1）中所求的B点坐标，进而求得结论；
解答 解：（1）∵反比例函数y=$\frac{k}{x}$的图象交于点A（-6，-3）和B（a，6），
∴-3=$\frac{k}{-6}$，6=$\frac{k}{a}$，
解得：k=18，a=3，
∴反比例函数的表达式为y=$\frac{18}{x}$，点B的坐标（3，6）；
（2）根据图象得当x＞3，或-6＜x＜0时，一次函数值大于反比例函数值．
点评 此题主要考查了待定系数法求出反比例函数、一次函数解析式，根据已知得出B点坐标是解题关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
如图，在△ABC中，AB=AC=5，BC=6，将△ABC绕点B逆时针旋转60°得到△A′BC′，连接A′C，则A′C的长为4+3$\sqrt{3}$．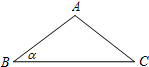
如图，底角为α的等腰△ABC绕着点B顺时针旋转，使得点A与边BC上的点D重合，点C与点E重合，联结AD、CE．已知tanα=$\frac{3}{4}$，AB=5，则CE=$\frac{8\sqrt{10}}{5}$．