题目内容
6.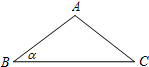 如图,底角为α的等腰△ABC绕着点B顺时针旋转,使得点A与边BC上的点D重合,点C与点E重合,联结AD、CE.已知tanα=$\frac{3}{4}$,AB=5,则CE=$\frac{8\sqrt{10}}{5}$.
如图,底角为α的等腰△ABC绕着点B顺时针旋转,使得点A与边BC上的点D重合,点C与点E重合,联结AD、CE.已知tanα=$\frac{3}{4}$,AB=5,则CE=$\frac{8\sqrt{10}}{5}$.
分析 如图,作AH⊥BC于H,EF⊥BC于F,则BH=CH,先利用三角形函数的定义和勾股定理可计算出BH=4,则BC=2BH=8,再根据旋转的性质得∠CBE=α,BE=BC=8,接着在Rt△BEF中利用三角函数的定义可计算出EF和BF,然后在Rt△CEF中利用勾股定理计算CE.
解答 解:如图,作AH⊥BC于H,EF⊥BC于F,则BH=CH,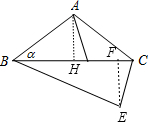
在Rt△ABH中,tan∠ABH=tanα=$\frac{AH}{BH}$=$\frac{3}{4}$,
设AH=3t,则BH=4t,
∴AB=$\sqrt{(3t)^{2}+(4t)^{2}}$=5t,
∴5t=5,解得t=1,
∴BC=2BH=8,
∵等腰△ABC绕着点B顺时针旋转,使得点A与边BC上的点D重合,
∴∠CBE=α,BE=BC=8,
在Rt△BEF中,tan∠EAF=tanα=$\frac{EF}{BF}$=$\frac{3}{4}$,
设AH=3x,则BH=4x,BE=5x,
∴5x=8,解得x=$\frac{8}{5}$,
∴EF=$\frac{24}{5}$,BF=$\frac{32}{5}$,
∴CF=8-$\frac{32}{5}$=$\frac{8}{5}$,
在Rt△CEF中,CE=$\sqrt{(\frac{8}{5})^{2}+(\frac{24}{5})^{2}}$=$\frac{8\sqrt{10}}{5}$.
故答案为$\frac{8\sqrt{10}}{5}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键作EF⊥BC构建直角三角形.

练习册系列答案
相关题目
1.下列运动属于平移的是( )
| A. | 看书时候翻页 | B. | 人随着电梯在运动 | ||
| C. | 士兵听从口令向后转 | D. | 汽车到路口转弯 |
11. 如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
 如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
18.已知2x3yn-1和-x3my2是同类项,则式子m-n的值是( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |
15.王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是0.25;(精确到0.01)
(2)估算袋中白球的个数.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
| 摸到黑球的频率$\frac{m}{n}$ | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 | 0.251 |
(2)估算袋中白球的个数.
 如图所示,OA垂直平分PM,OB垂直平分PN,且MN交OA,OB于C,D,MN=8cm,则△PCD的周长为8cm.
如图所示,OA垂直平分PM,OB垂直平分PN,且MN交OA,OB于C,D,MN=8cm,则△PCD的周长为8cm. 如图,一次函数与反比例函数y=$\frac{k}{x}$的图象交于点A(-6,-3)和B(a,6)
如图,一次函数与反比例函数y=$\frac{k}{x}$的图象交于点A(-6,-3)和B(a,6)