题目内容
19. 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$.
如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$.
分析 连结CC′,A′C交BC于O点,如图,利用旋转的性质得BC=BC′=6,∠CBC′=60°,A′B=AB=AC=A′C′=5,则可判断△BCC′为等边三角形,接着利用线段垂直平分线定理的逆定理说明A′C垂直平分B′C,则BO=$\frac{1}{2}$BC′=3,然后利用勾股定理计算出A′O,利用三角函数计算出OC,最后计算A′O+OC即可.
解答 解: 连结CC′,A′C交BC于O点,如图,
连结CC′,A′C交BC于O点,如图,
∵△ABC绕点B逆时针旋转60°得到△A′BC′,
∴BC=BC′=6,∠CBC′=60°,A′B=AB=AC=A′C′=5,
∴△BCC′为等边三角形,
∴CB=CB′,
而A′B=A′C′,
∴A′C垂直平分B′C,
∴BO=$\frac{1}{2}$BC′=3,
在Rt△A′OB中,A′O=$\sqrt{A′{B}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
在Rt△OBC中,∵tsin∠CBO=sin60°=$\frac{OC}{BC}$,
∴OC=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴A′C=A′O+OC=4+3$\sqrt{3}$.
故答案为4+3$\sqrt{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是证明△BCC′为等边三角形和A′C⊥BC′.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
11. 如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
 如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
 如图,OA=2,OB=3,将△AOB绕点A旋转,得△ADE,当点D落在AB上时,求点D的坐标.
如图,OA=2,OB=3,将△AOB绕点A旋转,得△ADE,当点D落在AB上时,求点D的坐标.
 如图,一次函数与反比例函数y=$\frac{k}{x}$的图象交于点A(-6,-3)和B(a,6)
如图,一次函数与反比例函数y=$\frac{k}{x}$的图象交于点A(-6,-3)和B(a,6)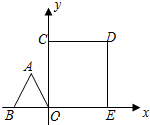 如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是11-2$\sqrt{3}$.
如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是11-2$\sqrt{3}$.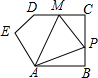 在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )
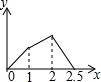
在五边形ABCDE中,∠B=90°,AB=BC=CD=1,AB∥CD,M是CD边的中点,点P由点A出发,按A→B→C→M的顺序运动.设点P经过的路程x为自变量,△APM的面积为y,则函数y的大致图象是( )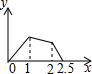
 完成下列各题:
完成下列各题: