题目内容
2. 如图,⊙O中,弧MAN的度数为320°,则圆周角∠MAN的度数是20°.
如图,⊙O中,弧MAN的度数为320°,则圆周角∠MAN的度数是20°.
分析 首先连接OM,ON,由⊙O中,弧MAN的度数为320°,根据弧与圆心角的关系,即可求得∠MON的度数,然后由圆周角定理,求得圆周角∠MAN的度数.
解答  解:连接OM,ON,
解:连接OM,ON,
∵⊙O中,弧MAN的度数为320°,
∴劣弧MN的度数为:360°-320°=40°,
∴∠MON=40°,
∴∠MAN=$\frac{1}{2}$∠MON=20°.
故答案为:20°.
点评 此题考查了圆周角定理以及弧与圆心角的关系.注意在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
12.工地调来72人参加挖土和运土,已知3人挖出的土1人恰好能全部运走,怎样调动劳动力才能使挖出的土能及时运走.解决此问题,可设派x人挖土,其它的人运土,可列方程( )
| A. | $\frac{72-x}{x}$=$\frac{1}{3}$ | B. | 72-x=3x | C. | x+3x=72 | D. | $\frac{x}{72-x}$=$\frac{1}{3}$ |
17.方程x$\sqrt{2-x}$=$\sqrt{2-x}$的解是( )
| A. | x1=2,x1=1,x3=-1 | B. | x1=2,x2=1 | C. | x1=2,x2=-1 | D. | x1=1,x2=-1 |
14.已知⊙O1与⊙O2的半径分别为3cm和4cm,两元的圆心距为7cm,则两圆的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内含 |
11.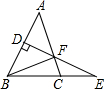 如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )
 如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )| A. | 16cm,40° | B. | 8cm,50° | C. | 16cm,50° | D. | 8cm,40° |
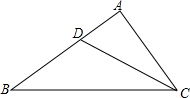 如图,△ABC中,已知∠A=2∠B,CD是∠ACB的平分线,试说明BC=AD+AC.(提示:在BC边上取点E,使EC=AC,联结DE).
如图,△ABC中,已知∠A=2∠B,CD是∠ACB的平分线,试说明BC=AD+AC.(提示:在BC边上取点E,使EC=AC,联结DE).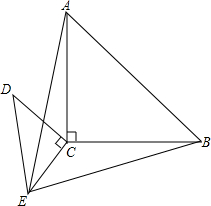 把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC
把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC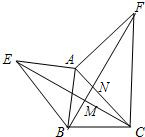 如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.
如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.