题目内容
12.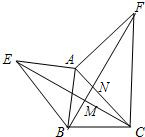 如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.
如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.
分析 首先根据边边边定理,证明△EAC≌△BAF.根据全等三角形对应角相等可得∠AFB=∠ACE,又∠ANF=∠CNM,所以∠CMF=∠CAF.
解答 证明:在△EAC和△BAF中,
$\left\{\begin{array}{l}{EC=BF}\\{AF=AC}\\{AE=AB}\end{array}\right.$,
∴△EAC≌△BAF(SSS),
∴∠AFB=∠ACE,
又∵∠ANF=∠CNM,
∴∠CMF=∠CAF.
点评 本题考查全等三角形的判定与性质定理.解决本题需要同学们对全等三角形的性质与判定要全面掌握,并做到灵活运用的能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2. 如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )
 如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )| A. | 13 | B. | $\frac{15}{2}$ | C. | $\frac{27}{2}$ | D. | 12 |
 如图,⊙O中,弧MAN的度数为320°,则圆周角∠MAN的度数是20°.
如图,⊙O中,弧MAN的度数为320°,则圆周角∠MAN的度数是20°.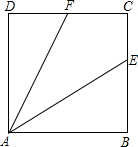 如图,正方形ABCD中,E为BC上一点.
如图,正方形ABCD中,E为BC上一点. 如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明: 如图,AB=AC,点F、E分别是AB、AC的中点.求证:∠1=∠2.
如图,AB=AC,点F、E分别是AB、AC的中点.求证:∠1=∠2.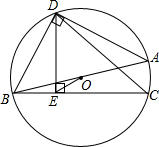 如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.
如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.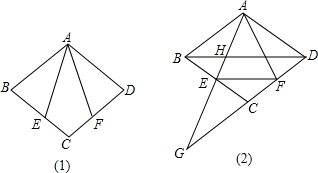
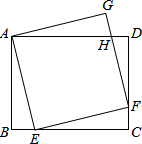 如图,在矩形ABCD中,AB=4,BC=5.点E在边BC上,以AE为边作正方形AEFG,顶点F恰好在边CD上,FG与AD交于点H.则DH的长为$\frac{3}{4}$.
如图,在矩形ABCD中,AB=4,BC=5.点E在边BC上,以AE为边作正方形AEFG,顶点F恰好在边CD上,FG与AD交于点H.则DH的长为$\frac{3}{4}$.