题目内容
7.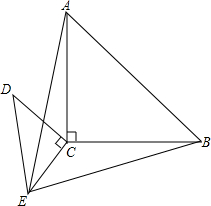 把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC
把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC(1)请你在图中连接两条线段,构造两个全等三角形.
(2)连接的这两条线段相等吗?垂直吗?
分析 (1)连接AE、BD,先求出∠ACE=∠BCD,由SAS即可证明△ACE≌△BCD;
(2)由△ACE≌△BCD,得出AE=BD,∠CAE=∠CBD,再由∠CBD+∠BMC=90°,∠BMC=∠AMD,证出∠ANM=90°,即可得出AE⊥BD.
解答 解:(1)连接AE、BD,如图所示: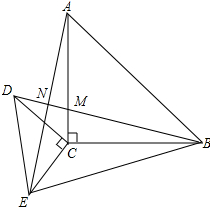 △ACE≌△BCD;
△ACE≌△BCD;
理由如下:∵∠ACB=∠DCE=90°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACE=∠BCD}&{\;}\\{EC=DC}&{\;}\end{array}\right.$,
∴△ACE≌△BCD(SAS);
(2)AE=BD,AE⊥D;理由如下:
由(1)得:△ACE≌△BCD,
∴AE=BD,∠CAE=∠CBD,
∵∠CBD+∠BMC=90°,∠BMC=∠AMD,
∴∠AMD+∠CAE=90°,
∴∠ANM=90°,
∴AE⊥BD.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质、垂线的判定;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
15.已知关于x的方程x2-2x+m-1=0,若方程的一个根为1,则m的值是( )
| A. | -2 | B. | 2 | C. | 0 | D. | 1 |
12.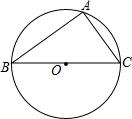 如图,已知AB是⊙O的直径,∠B=30°,则∠C的度数是( )
如图,已知AB是⊙O的直径,∠B=30°,则∠C的度数是( )
 如图,已知AB是⊙O的直径,∠B=30°,则∠C的度数是( )
如图,已知AB是⊙O的直径,∠B=30°,则∠C的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
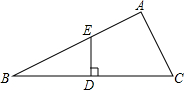 如图,已知在△ABC中,∠A=90°,D是BC中点,且DE⊥BC于D,交AB于E,求证:BE2-EA2=AC2.
如图,已知在△ABC中,∠A=90°,D是BC中点,且DE⊥BC于D,交AB于E,求证:BE2-EA2=AC2. 如图,⊙O中,弧MAN的度数为320°,则圆周角∠MAN的度数是20°.
如图,⊙O中,弧MAN的度数为320°,则圆周角∠MAN的度数是20°.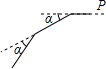 寒假里,小燕偶然发现爸爸手机有陀罗仪可用来测量方位,于是她来到小区一处广场上.如图,小燕从P点向西直走12米后,向左转,转动的角度为α=40度,再走12米,再左转40度,如此重复,最终小燕又回到点P,则小燕一共走了108米.
寒假里,小燕偶然发现爸爸手机有陀罗仪可用来测量方位,于是她来到小区一处广场上.如图,小燕从P点向西直走12米后,向左转,转动的角度为α=40度,再走12米,再左转40度,如此重复,最终小燕又回到点P,则小燕一共走了108米.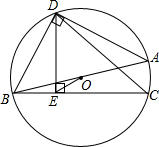 如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.
如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.