题目内容
10.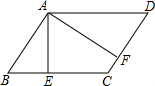 如图,已知:在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,且∠EAF=60°,BE=2cm,DF=3cm,求?ABCD的周长和面积.
如图,已知:在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,且∠EAF=60°,BE=2cm,DF=3cm,求?ABCD的周长和面积.
分析 由AE⊥BC,AF⊥CD,∠EAF=60°,根据四边形的内角和为360°,求得∠C;根据平行四边形的对边平行,可得∠B与∠C互补,即可求得∠B=60°,在直角三角形ABE中求得AB的长,同理求得AD的长,继而求得平行四边形ABCD的周长和面积.
解答 解:∵AE⊥BC,AF⊥CD,∠EAF=60°,
∴∠AEB=∠AEC=∠AFC=∠AFD=90°,
∴∠C=120°,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD∥BC,∠B=∠D,
∴∠B+∠C=180°,
∴∠B=∠D=60°,
∴∠BAE=∠FAD=30°,
∵BE=2cm,FD=3cm,
∴AB=4cm,BC=AD=6cm,AF=3$\sqrt{3}$,
∴?ABCD的周长为=2(AB+BC)=20cm,
S?ABCD=CD•AF=4×3$\sqrt{3}$=12$\sqrt{3}$cm2.
点评 此题考查了平行四边形的性质:平行四边形的对边平行且相等.还考查了直角三角形中30°角所对的直角边是斜边的一半,正确求得∠B和∠DAF的度数是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.点(4,-5)关于y轴的对称点的坐标是( )
| A. | (4,5) | B. | (-4,-5) | C. | (-4,5) | D. | (-5,4) |
5.已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则a+b的值是( )
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
15.反比例函数y=$\frac{-2}{x}$的图象上点A(2,m)到原点的距离AO等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{2}$ |