题目内容
7.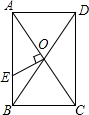 如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则AE=5.
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则AE=5.
分析 首先连接EC,由题意可得OE为对角线AC的垂直平分线,可得CE=AE,S△AOE=S△COE=5,继而可得$\frac{1}{2}$AE•BC=10,则可求得AE的长.
解答  解:连接EC,如图所示:
解:连接EC,如图所示:
由题意可得,OE为对角线AC的垂直平分线,
∴CE=AE,S△AOE=S△COE=5,
∴S△AEC=2S△AOE=10,
∴$\frac{1}{2}$AE•BC=10,
又∵BC=4,
∴AE=5,
故答案为:5.
点评 此题考查了矩形的性质、垂直平分线的性质、三角形的面积等知识;熟练掌握矩形性质与三角形面积的计算方法是解决问题的关键.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
17.给出四个数0,$\sqrt{2}$,-1,3,其中最小的是( )
| A. | -1 | B. | 0 | C. | $\sqrt{2}$ | D. | 3 |
15.反比例函数y=$\frac{-2}{x}$的图象上点A(2,m)到原点的距离AO等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 2$\sqrt{2}$ |
12.若点P是y轴上一动点,则点P到点A(-2,5)和B(-4,3)的距离之和最短时,点P的坐标为( )
| A. | (0,$\frac{8}{3}$) | B. | (0,-$\frac{8}{3}$) | C. | (0,$\frac{13}{3}$) | D. | (0,-$\frac{13}{3}$) |