题目内容
19．（1）解方程：x2-4x=0（2）化简：m（m+3）-（m+1）2，其中m=$\sqrt{2}$+1．
分析 （1）方程利用因式分解法求出解即可；
（2）原式利用单项式乘以多项式，以及完全平方公式化简，去括号合并得到最简结果，把m的值代入计算即可求出值．
解答 解：（1）方程x2-4x=0，
分解因式得：x（x-4）=0，
可得x=0或x-4=0，
解得：x1=0，x2=4；
（2）m2+3m-（m2+2m+1）
=m2+3m-m2-2m-1
=m-1，
当m=$\sqrt{2}$+1时，原式=$\sqrt{2}$+1-1=$\sqrt{2}$．
点评 此提考查了整式的混合运算-化简求值，以及解一元二次方程-因式分解法，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图所示，点P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长BP交边AD于点F，交CD的延长线于点G．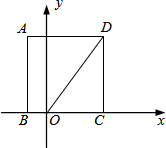
如图，正方形ABCD的顶点B、C都在直角坐标系的x轴上，若点B的坐标是（-1，0），OD=5，则点C的坐标是（3，0）．
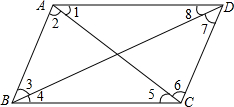如图，在图中标示的角∠1、∠2、∠3、∠4、∠5、∠6、∠7、∠8中，内错角有几对，它们分别是哪两条直线被哪两条直线所截而构成的？
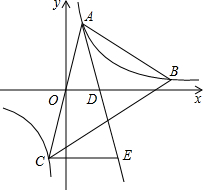如图，在平面直角坐标系xOy中，点A（$\frac{1}{2}$，2），B（3，n），在反比例函数y=$\frac{m}{x}$（m为常数）的图象上，连接AO并延长与图象的另一支有另一个交点为点C，过点A的直线l与x轴的交点为点D（1，0），过点C作CE∥x轴交直线l于点E．