题目内容
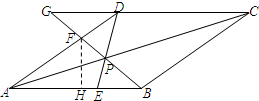
9. 如图所示,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.
如图所示,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.(1)求证:PB=PD;
(2)若已知$\frac{DF}{FA}$=$\frac{1}{2}$,请确定线段DP与线段PF之间满足的数量关系;并求当DP=6时,线段FG的长;
(3)在(2)的条件下,当△DGP是等腰三角形时,请直接写出tan∠DAB的值.
分析 (1)根据菱形的性质得出∠DAP=∠PAB,AD=AB,再利用全等三角形的判定得出△APB≌△APD;
(2)首先证明△DFP≌△BEP,进而得出$\frac{DG}{AB}$=$\frac{1}{2}$,$\frac{BE}{AB}$=$\frac{1}{3}$,进而得出 $\frac{DP}{PE}$=$\frac{DG}{EB}$,即 $\frac{3}{2}$=$\frac{DP}{PF}$,即可得出答案;
(3)由(1)证得△APB≌△APD,得到∠ABP=∠ADP,根据平行线的性质,得到∠G=∠ABP,①若DG=PG根据△DGP∽△EBP,得DG=$\frac{9}{2}$a,由勾股定理得到FH=$\sqrt{(6a)2-x2}$=$\frac{20\sqrt{2}}{9}$a
于是得到结论,②若DG=DP,设DG=DP=3m,则PB=3m,PE=BE=PF=2m,AB=AD=2DG=6m,AF=4m,BF=5m,设AH=x,求得FH=$\sqrt{(4m)2-x2}$=$\frac{5\sqrt{7}}{4}$m,得到tan∠DAB=$\frac{FH}{AH}$=$\frac{5\sqrt{7}}{9}$.
解答 (1)证明:∵四边形ABCD是菱形,
∴AB=AD,AC平分∠DAB,
∴∠DAP=∠BAP,
在△APB和△APD中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAP=∠DAP}\\{AP=AP}\end{array}\right.$,
∴△APB≌△APD,
∴PB=PD;
(2)∵四边形ABCD是菱形,∴AD∥BC,AD=BC,
∴△AFP∽△CBP,
∴$\frac{AF}{BC}$=$\frac{FP}{BP}$
∵$\frac{DF}{FA}$=$\frac{1}{2}$,
∴$\frac{AF}{BC}$=$\frac{2}{3}$,
∴$\frac{FP}{BP}$=$\frac{2}{3}$
由(1)知PB=PD,
∴$\frac{PF}{PD}$=$\frac{2}{3}$,
∴PF=$\frac{2}{3}$PD,
当DP=6时,PF=$\frac{2}{3}$×6=4,
∴FB=FP+PB=4+6=10,
∵DG∥AB,
∴△DFG∽△AFB
∴$\frac{FG}{FB}$=$\frac{FD}{FA}$=$\frac{1}{2}$,
∴FG=$\frac{1}{2}$×10=5
即线段FG的长为5;
∴线段DP与线段PF满足的数量关系是PF=$\frac{2}{3}$PD;当DP=6时,FG的长为5;
(3) 由(1)证得△APB≌△APD,
由(1)证得△APB≌△APD,
∴∠ABP=∠ADP,
∵GC∥AB,
∴∠G=∠ABP,
∴∠ADP=∠G,
∴∠GDP>∠G,
∴PD≠PG.
①若DG=PG,
∵DG∥AB,
∴△DGP∽△EBP,
∴PB=EB,
由(2)知$\frac{PF}{PD}$=$\frac{2}{3}$,设PF=2a,
则PB=BE=PD=3a,PE=PF=2a,BF=5a,
由△DGP∽△EBP,得DG=$\frac{9}{2}$a,
∴AB=AD=2DG=9a,
∴AF=6a,
作FH⊥AB于H,设AH=x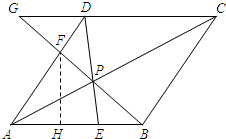 则(6a)2-x2=(5a)2-(9a-x)2
则(6a)2-x2=(5a)2-(9a-x)2
解得x=$\frac{46}{9}$a,∴FH=$\sqrt{(6a)2-x2}$=$\frac{20\sqrt{2}}{9}$a
∴tan∠DAB=$\frac{FH}{AH}$=$\frac{10\sqrt{2}}{23}$
②若DG=DP,
设DG=DP=3m,则PB=3m,PE=BE=PF=2m,
AB=AD=2DG=6m,AF=4m,BF=5m,
设AH=x,
∴(4m)2-x2=(5m)2-(6m-x)2,
解得x=$\frac{9}{4}$m,
∴FH=$\sqrt{(4m)2-x2}$=$\frac{5\sqrt{7}}{4}$m,
∴tan∠DAB=$\frac{FH}{AH}$=$\frac{5\sqrt{7}}{9}$.
点评 此题主要考查了相似三角形的判定与性质,全等三角形的判定与性质,勾股定理,锐角三角函数,平行线的性质,菱形的性质,正确的作出辅助线是解题的关键.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案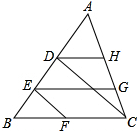 如图:DH∥EG∥BC,DC∥EF,那么与∠EFC互补的角的个数为( )
如图:DH∥EG∥BC,DC∥EF,那么与∠EFC互补的角的个数为( )| A. | 1个 | B. | 4个 | C. | 6个 | D. | 8 |
| A. | 2,-1 | B. | -2,-1 | C. | 2,1 | D. | -2,1 |
| A. | a | B. | a2 | C. | -a2 | D. | a3 |
 如图,把一块含有30°的三角板的两个顶点放在一长方形纸片的对边上.如果∠1=20°,那么∠2的度数是40度.
如图,把一块含有30°的三角板的两个顶点放在一长方形纸片的对边上.如果∠1=20°,那么∠2的度数是40度.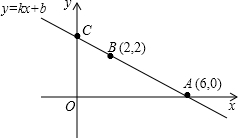 如图,一次函数y=kx+b的图象经过点A(6,0),点B(2,2),且与y轴相交于点C.请根据以上信息(不再添加其他条件),提出一个问题并尝试解答.你提出的问题是点C的坐标是什么;并请写出你的解答过程.
如图,一次函数y=kx+b的图象经过点A(6,0),点B(2,2),且与y轴相交于点C.请根据以上信息(不再添加其他条件),提出一个问题并尝试解答.你提出的问题是点C的坐标是什么;并请写出你的解答过程.