题目内容
20.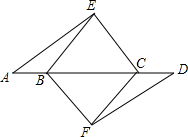 如图,AE∥DF,CE∥BF,AB=CD,求证:BE∥CF.
如图,AE∥DF,CE∥BF,AB=CD,求证:BE∥CF.
分析 由AE∥DF,CE∥BF,可知∠A=∠D,∠DBF=∠ACE,由AB=CD,可知AC=DB,根据ASA可证△ACE≌△DBF,则BF=CE,于是四边形BFCE是平行四边形,故BE∥CF.
解答 证明:∵AE∥DF,CE∥BF,
∴∠A=∠D,∠DBF=∠ACE,
∵AB=CD,
∴AC=DB,
在△ACE和△DBF中,
$\left\{\begin{array}{l}{∠A=∠D}\\{AC=DB}\\{∠DBF=∠ACE}\end{array}\right.$,
∴△ACE≌△DBF,
∴BF=CE,
∴四边形BFCE是平行四边形,
∴BE∥CF.
点评 本题主要考查了全等三角形的判定与性质以及平行四边形的判定与性质,证明△ACE≌△DBF是解决问题的关键.

练习册系列答案
相关题目
15.若|a|=5,|b|=2,a<b,则a,b分别为( )
| A. | 5,-2 | B. | -5,-2 | C. | -5,2 | D. | -5,-2或-5,2 |
 如图,四边形ABCD三边切⊙O于F、G、H,说明AB+CD与BC+AD的大小关系.
如图,四边形ABCD三边切⊙O于F、G、H,说明AB+CD与BC+AD的大小关系.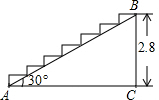 如图,某宾馆重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示(单位:米),求购买地毯至少需要多少元.
如图,某宾馆重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示(单位:米),求购买地毯至少需要多少元. 如图所示,AB是半圆的直径,∠ABC=90°,AC交半圆于点D.若AD=6,DC=2,求:
如图所示,AB是半圆的直径,∠ABC=90°,AC交半圆于点D.若AD=6,DC=2,求: 如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,l4和l1,l2相交于C,D两点,点P在直线AB上,
如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,l4和l1,l2相交于C,D两点,点P在直线AB上,