题目内容
11．
如图，四边形ABCD三边切⊙O于F、G、H，说明AB+CD与BC+AD的大小关系．
分析 过点A作⊙O的切线，切点为点M，交BC于点E，根据从圆外一点引圆的两条切线，它们的切线长相等，将线段和转化，继而利用三角形三边关系可作出判断．
解答 
解：过点A作⊙O的切线，切点为点M，交BC于点E，
由题意得，DG=DH，CG=CF，AH=AM，EM=EF，
从而可得BC+AD=BF+AH+CD=BE+AE+CD，
在△ABE中，BE+AE＞AB，
则BE+AE+CD＞AB+CD．
即AB+CD＜BC+AD．
点评 本题考查了切线长定理，解答本题的关键是作出辅助线，利用三角形的三边关系确定大小关系，注意掌握切线长定理的内容．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
1．下列关于抛物线y=-x2-2的结论，正确的是（ ）
| A． | 与x轴有两个交点 | B． | 开口向上 | ||
| C． | 与y轴的交点坐标（0，2） | D． | 顶点坐标是（0，-2） |
如图，过⊙O内一点P画弦AB使P是AB的中点．
19．已知x2-3x+1=0，则$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2}$=（ ）
| A． | 3 | B． | 4 | C． | $\sqrt{5}$ | D． | $\sqrt{7}$ |
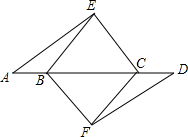如图，AE∥DF，CE∥BF，AB=CD，求证：BE∥CF．