题目内容
14.化简$\frac{{-3\sqrt{2}}}{{\sqrt{27}}}$的结果是( )| A. | -$\frac{{\sqrt{2}}}{3}$ | B. | -$\frac{2}{{\sqrt{3}}}$ | C. | -$\frac{{\sqrt{6}}}{3}$ | D. | -$\sqrt{2}$ |
分析 直接进行分母有理化即可求解.
解答 解:原式=$\frac{-3\sqrt{2}×\sqrt{27}}{27}$
=-$\frac{\sqrt{6}}{3}$.
点评 本题考查了二次根式的乘除法,解答本题的关键是进行分母有理化.

练习册系列答案
相关题目
2.若三角形两边的长分别是8和6,第三边的长是方程x2-2x=10(x-2)的一个实数根,则这个三角形的周长是( )
| A. | 24 | B. | 24或16 | C. | 16 | D. | 22 |
9.下列关于二次函数的说法错误的是( )
| A. | 抛物线y=-2x2+3x+1的对称轴是直线x=$\frac{3}{4}$ | |
| B. | 点A(3,0)不在抛物线y=x2-2x-3的图象上 | |
| C. | 二次函数y=(x+2)2-2的顶点坐标是(-2,-2) | |
| D. | 函数y=2x2+4x-3的图象的最低点在(-1,-5) |
19. 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
 如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )
如图以数轴的单位长线段为边作一个正方形,以数轴的原点为旋转中心,将过原点的对角线顺时针旋转,使对角线的另一端点落在数轴正半轴的点A处,则点A表示的数是( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 1.4 |
3.若$\sqrt{x-1}$+(y+3)2=0,则x-y的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -7 |
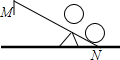 周末小威帮奶奶收拾菜园中的石头,有一块石头较大,需要借助木棒撬走,如图所示,O是支点,当用力压木棒的M端时,木棒绕点O转动,另一端N向上翘起,石头就被撬动.小威要想是这块石头滚动,木棒的N端必须向上跳起5cm.若3ON=OM,则要使这块石头滚动,至少要将木棒的M端向下压( )
周末小威帮奶奶收拾菜园中的石头,有一块石头较大,需要借助木棒撬走,如图所示,O是支点,当用力压木棒的M端时,木棒绕点O转动,另一端N向上翘起,石头就被撬动.小威要想是这块石头滚动,木棒的N端必须向上跳起5cm.若3ON=OM,则要使这块石头滚动,至少要将木棒的M端向下压( )