题目内容
2.若三角形两边的长分别是8和6,第三边的长是方程x2-2x=10(x-2)的一个实数根,则这个三角形的周长是( )| A. | 24 | B. | 24或16 | C. | 16 | D. | 22 |
分析 先解方程得出方程的根,根据三角形的三边关系定理舍去一个根,从而得出三角形的周长.
解答 解:∵第三边的长是方程x2-2x=10(x-2)的一个实数根,
∴x1=2,x2=10,
∴当第三边为2时,2+6=8,舍去,
∴三角形的周长为8+6+10=24.
故选A.
点评 本题考查了一元二次方程的解法以及三角形的三边关系定理,是基础题比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.把一元二次方程6x2-3=4x(2x-1)化为一般形式是( )
| A. | -2x2-4x+3=0 | B. | 2x2+4x-3=0 | C. | 2x2-4x+3=0 | D. | 2x2-4x-3=0 |
14.化简$\frac{{-3\sqrt{2}}}{{\sqrt{27}}}$的结果是( )
| A. | -$\frac{{\sqrt{2}}}{3}$ | B. | -$\frac{2}{{\sqrt{3}}}$ | C. | -$\frac{{\sqrt{6}}}{3}$ | D. | -$\sqrt{2}$ |
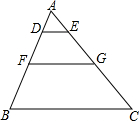 如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.
如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.