题目内容
3.已知a、b都为正整数(a≤b),且$\sqrt{a}$+$\sqrt{b}$=$\sqrt{72}$,则a、b的值分别为2,50或8,32或18,18.分析 先把$\sqrt{72}$化为最减二次根式,再根据合并同类项的法则进行解答即可.
解答 解:∵$\sqrt{72}$=6$\sqrt{2}$,a、b都为正整数,
∴当$\sqrt{a}$=$\sqrt{2}$,即a=2时,$\sqrt{b}$=5$\sqrt{2}$,故b=50;
当$\sqrt{a}$=2$\sqrt{2}$,即a=8时,$\sqrt{b}$=4$\sqrt{2}$,故b=32;
当$\sqrt{a}$=3$\sqrt{2}$,即a=18时,$\sqrt{b}$=8$\sqrt{2}$,故b=18.
综上所述,ab的值分别为:2,50或8,32或18,18.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.化简$\frac{{-3\sqrt{2}}}{{\sqrt{27}}}$的结果是( )
| A. | -$\frac{{\sqrt{2}}}{3}$ | B. | -$\frac{2}{{\sqrt{3}}}$ | C. | -$\frac{{\sqrt{6}}}{3}$ | D. | -$\sqrt{2}$ |
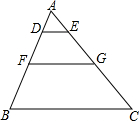 如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11.
如图,在△ABC中,DE∥FG∥BC,且AD:DF:BF=2:3:4,已知△ABC的周长为27,BC=9,则四边形DEGF的周长为11. 如图所示,△ABC中,D点在AC上,E点在BC上,且满足△ABD≌△EBD,△DBE≌△DCE,求∠A和∠C的度数.
如图所示,△ABC中,D点在AC上,E点在BC上,且满足△ABD≌△EBD,△DBE≌△DCE,求∠A和∠C的度数.