题目内容
2.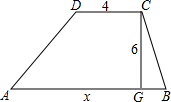 如图,梯形ABCD上底的长是4,下底的长是x,高是6.
如图,梯形ABCD上底的长是4,下底的长是x,高是6.(1)求梯形ABCD的面积y与下底长x之间的关系式;
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
(3)x每增加1时,y如何变化?说明你的理由.
分析 (1)利用梯形面积公式得出y与x之间的关系;
(2)结合关系式列表计算得出相关数据;
(3)利用(1)中关系式,进而得出x每增加1时,y的变化.
解答 解:(1)∵梯形ABCD上底的长是4,下底的长是x,高是6,
∴梯形ABCD的面积y与下底长x之间的关系式为:y=$\frac{1}{2}$(4+x)×6=12-3x;
(2)
| x | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| y | -18 | -21 | -24 | -27 | -30 | -33 | -36 |
理由:y1=12-3x,y2=12-3(x+1)=12-3x-3=9-3x,
y2-y1=9-3x-(12-3x)=-3,即x每增加1时,y减小3.
点评 此题主要考查了函数关系式以及函数的变化,正确得出函数关系式是解题关键.

练习册系列答案
相关题目
10.(-1)2015的值是( )
| A. | -1 | B. | 1 | C. | -2015 | D. | 2015 |
14.三角形中,三个内角的比为1:3:6,它的三个外角的比为( )
| A. | 1:3:6 | B. | 6:3:1 | C. | 9:7:4 | D. | 4:7:9 |
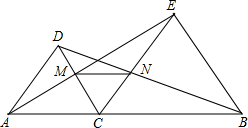 已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.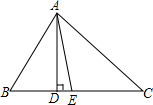 如图,在△ABC中,∠B=63°,∠C=47°,AD和AE分别是它的高和角平分线,则
如图,在△ABC中,∠B=63°,∠C=47°,AD和AE分别是它的高和角平分线,则 如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N=360°或540°或720°.
如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N=360°或540°或720°.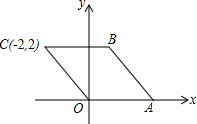 如图,在平面直角坐标系中,菱形OABC的顶点C的坐标为(-2,2),则顶点A、B的坐标分别为(2$\sqrt{2}$,0),(-2+2$\sqrt{2}$,2).
如图,在平面直角坐标系中,菱形OABC的顶点C的坐标为(-2,2),则顶点A、B的坐标分别为(2$\sqrt{2}$,0),(-2+2$\sqrt{2}$,2).