题目内容
12.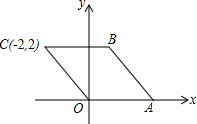 如图,在平面直角坐标系中,菱形OABC的顶点C的坐标为(-2,2),则顶点A、B的坐标分别为(2$\sqrt{2}$,0),(-2+2$\sqrt{2}$,2).
如图,在平面直角坐标系中,菱形OABC的顶点C的坐标为(-2,2),则顶点A、B的坐标分别为(2$\sqrt{2}$,0),(-2+2$\sqrt{2}$,2).
分析 先根据点C的坐标得出OC的长度,然后由菱形的性质可得出OC=OA=CB,从而可得出点A及点B的坐标.
解答 解:由题意得:OC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴OC=OA=CB,
∴点A的坐标为(2$\sqrt{2}$,0),点B的坐标为(-2+2$\sqrt{2}$,2).
故答案为:(2$\sqrt{2}$,0),(-2+2$\sqrt{2}$,2).
点评 本题考查菱形的性质及平移的性质,根据点C的坐标得出OC的长度是关键,另外要学会线段长度与点的坐标的转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.一组数据为6,12,12,15,9,27,12,15,3,24,其众数、中位数及平均数分别是( )
| A. | 12,12,18 | B. | 12,12,13.5 | C. | 12,18,13.5 | D. | 15,18,13.5 |
17.下列命题中真命题有几个( )
①三角形的任意两边之和都大于第三边;②三角形的任意两角之和都大于第三个角;
③同位角都相等;④若a=b,则|a|=|b|;⑤相等的角都是直角;
⑥同角的补角不一定相等;⑦一个三角形中最大的角不会小于60°.
①三角形的任意两边之和都大于第三边;②三角形的任意两角之和都大于第三个角;
③同位角都相等;④若a=b,则|a|=|b|;⑤相等的角都是直角;
⑥同角的补角不一定相等;⑦一个三角形中最大的角不会小于60°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.下列图形中,属于中心对称图形的是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 菱形 | D. | 对角互补的四边形 |
1.据平凉市旅游局统计,2015年十一黄金周期间,平凉市接待游客38万人,实现旅游收入16000000元.将16000000用科学记数法表示应为( )
| A. | 0.16×108 | B. | 1.6×107 | C. | 16×106 | D. | 1.6×106 |
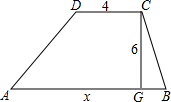 如图,梯形ABCD上底的长是4,下底的长是x,高是6.
如图,梯形ABCD上底的长是4,下底的长是x,高是6.
 如图,两条直线被三条平行线所截,若AB=4,BC=6,EF=5,则DF=$\frac{25}{3}$.
如图,两条直线被三条平行线所截,若AB=4,BC=6,EF=5,则DF=$\frac{25}{3}$. 如图在平面直角坐标系中,△OAB的顶点坐标分别是O(0,0),A(2,4),B(6,0).
如图在平面直角坐标系中,△OAB的顶点坐标分别是O(0,0),A(2,4),B(6,0).