题目内容
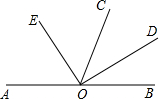 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.(1)若∠BOC=68°,求∠COD和∠EOC的度数;
(2)小明说:不管∠BOC是多少度,∠DOE都是90°.你认为小明说得有道理吗?请你通过计算说明理由.
考点:角平分线的定义
专题:
分析:(1)根据角平分线的定义求出∠COD的度数即可,先求出∠AOC的度数,再根据角平分线的定义解答;
(2)根据角平分线的定义表示出∠COD与∠EOC,然后整理即可得解.
(2)根据角平分线的定义表示出∠COD与∠EOC,然后整理即可得解.
解答:解:(1)∵OD平分∠BOC,∠BOC=68°,
∴∠COD=
∠BOC=
×68°=34°,
∵∠BOC=68°,
∴∠AOC=180°-∠BOC=180°-68°=112°,
∵OE平分∠AOC,
∴∠EOC=
∠AOC=
×112°=56°;
(2)小明说的有道理,理由如下:
∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=
∠BOC,∠EOC=
∠AOC,
∴∠COD+∠EOC=
(∠BOC+∠AOC)=×180°=90°,
即∠DOE=90°.
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BOC=68°,
∴∠AOC=180°-∠BOC=180°-68°=112°,
∵OE平分∠AOC,
∴∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)小明说的有道理,理由如下:
∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COD+∠EOC=
| 1 |
| 2 |
即∠DOE=90°.
点评:本题考查了余角和补角的概念,角度的计算,以及角平分线的定义,准确识图并熟记概念是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以下列各组数为边的三角形不是直角三角形的是( )
| A、5,6,9 |
| B、5,3,4 |
| C、24,10,26 |
| D、60,11,61 |
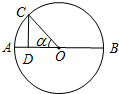 如图,AB为⊙O的直径,D为AB上一点,且AB=6AD,CD⊥AB于D,C在⊙O上,设∠COD=α,则tan
如图,AB为⊙O的直径,D为AB上一点,且AB=6AD,CD⊥AB于D,C在⊙O上,设∠COD=α,则tan| α |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y=
x2上,则y1,y2,y3的大小关系是( )
| 2 |
| 3 |
| A、y1<y2<y3 |
| B、y1>y2>y3 |
| C、y1<y3<y2 |
| D、y2<y3<y1 |
根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断二次函数的解析式为( )
| x | … | -1 | 0 | 1 | 2 | … | ||||
| y | … | -1 | -
| -2 | -
| … |
A、y=
| ||||||
B、y=
| ||||||
C、y=-
| ||||||
D、y=-
|